题目内容
【题目】欧几里得在《几何原本》中,记载了用图解法解方程![]() 的方法,类似地可以用折纸的方法求方程
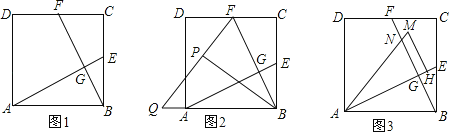
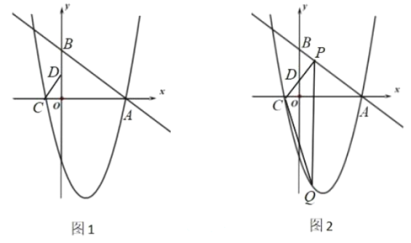
的方法,类似地可以用折纸的方法求方程![]() 的一个正根。下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形的纸片
的一个正根。下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,再折出线段
,再折出线段![]() ,然后通过折叠使
,然后通过折叠使![]() 落在线段
落在线段![]() 上,折出点
上,折出点![]() 的新位置
的新位置![]() ,因而
,因而![]() ,类似地,在
,类似地,在![]() 上折出点
上折出点![]() 使
使![]() 。此时,
。此时,![]() 的长度可以用来表示方程
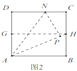
的长度可以用来表示方程![]() 的一个正根;乙:如图2,裁一张边长为1的正方形的纸片
的一个正根;乙:如图2,裁一张边长为1的正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,再折出线段
,再折出线段![]() N,然后通过沿线段
N,然后通过沿线段![]() 折叠使
折叠使![]() 落在线段
落在线段![]() 上,折出点
上,折出点![]() 的新位置
的新位置![]() ,因而
,因而![]() 。此时,
。此时,![]() 的长度可以用来表示方程
的长度可以用来表示方程![]() 的一个正根;甲、乙两人的做法和结果( )。
的一个正根;甲、乙两人的做法和结果( )。

A.甲对,乙错B.乙对,甲错C.甲乙都对D.甲乙都错
【答案】C
【解析】
图1中,设AM=AF=x,列出关于x的等式判断即可,图2中,设DN为x,列出关于x的等式判断即可.
在图1中,
∵正方形ABCD的边长为1,AM=AF=x,
∴BE=EF=![]() ,AE=
,AE=![]() ,
,
在Rt△ABE中,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的长度可以用来表示方程
的长度可以用来表示方程![]() 的一个正根,
的一个正根,
故甲同学的做法正确;
在图2中,连接NH,
∵正方形边长为1,H是CB中点,
∴BH=CH=![]() ,
,
∴![]() ,
,
∵折叠,
∴AP=AD=1,
∴HP=![]() ,
,
设DN为x,
则NP=x,CN=1-x,
∴在Rt△NPH中,
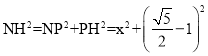 ,
,
在Rt△NCH中,
![]() ,
,
∴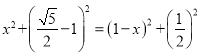 ,
,
解得:![]() ,
,
把![]() 代入
代入![]() 中,等式成立,
中,等式成立,
∴![]() 的长度可以用来表示方程
的长度可以用来表示方程![]() 的1个正根,
的1个正根,
故乙同学做法正确;
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目