题目内容
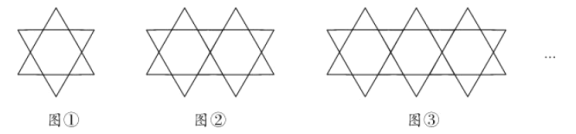
【题目】将大小相同的正三角形按如图所示的规律拼图案，其中第①个图案中有6个小三角形和1个正六边形；第②个图案中有10个小三角形和2个正六边形；第③个图案中有14个小三角形和3个正六边形；…；按此规律排列下去，已知一个正六边形的面积为
，一个小三角形的面积为
，则第③个图案中所有的小三角形和正六边形的面积之和为______．（结果用含、的代数式表示）
【答案】
【解析】
由题意得出规律为每增加一个正六边形，则增加4个小三角形，即可得出答案．
由题意：第①个图案中有6个小三角形和1个正六边形；
第②个图案中有10=6+4×1=10个小三角形和2个正六边形；
第③个图案中有14=6+4×2=14个小三角形和3个正六边形；
∵一个正六边形的面积为
，一个小三角形的面积为
，
∴第③个图案中所有的小三角形和正六边形的面积之和为：；
故答案为：．
练习册系列答案
相关题目
【题目】某校举行“诵读经典”朗诵比赛，把比赛成绩分为四个等次：
优秀，
.良好，
.一般，
.较差，从参加比赛的学生中随机抽取部分学生的成绩进行调查，并根据调查结果制作了如下的统计图表（不完整）：
学生朗读比赛成绩频数分布表
等次 | 频数 | 频率 |
|
| 0.1 |
| 20 | 0.4 |
|
|
|
| 10 | 0.2 |
合计 | 1 |
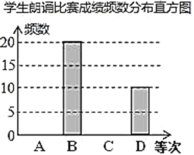
（1）这次共调查了______名学生，表中
_____，
_____，
_____；
（2）补全频数分布直方图；
（3）若抽查的学生中，等次中有2名女生，其他为男生，从等次中选取两名同学参加市中学生朗诵比赛，求恰好选取一名男生和一名女生的概率．
