题目内容
(12分)如图,在Rt△ABC中,∠C=90°,AC=BC=4cm,点D为AC边上一
点,且AD=3cm,动点E从点A出发,以1cm/s的速度沿线段AB向终点B运动,运动
时间为x s.作∠DEF=45°,与边BC相交于点F.设BF长为ycm.
(1)当x= ▲ s时,DE⊥AB;
(2)求在点E运动过程中,y与x之间的函数关系式及点F运动路线的长;
(3)当△BEF为等腰三角形时,求x的值.
点,且AD=3cm,动点E从点A出发,以1cm/s的速度沿线段AB向终点B运动,运动
时间为x s.作∠DEF=45°,与边BC相交于点F.设BF长为ycm.
(1)当x= ▲ s时,DE⊥AB;
(2)求在点E运动过程中,y与x之间的函数关系式及点F运动路线的长;
(3)当△BEF为等腰三角形时,求x的值.

解:(1)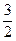
 ············································································ 2分
············································································ 2分
(2)∵在△ABC中,∠C=90°,AC=BC=4.
∴∠A=∠B=45°,AB=4 ,∴∠ADE+∠AED=135°;
,∴∠ADE+∠AED=135°;
又∵∠DEF=45°,∴∠BEF+∠AED=135°,∴∠ADE=∠BEF;
∴△ADE∽△BEF····················································································· 4分
∴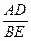 =
=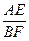 ,
,
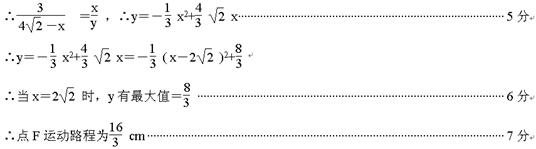
(3)这里有三种情况:
①如图,若EF=BF,则∠B=∠BEF;
又∵△ADE∽△BEF,∴∠A=∠ADE=45°
∴∠AED=90°,∴AE=DE=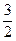
 ,
,
∵动点E的速度为1cm/s,∴此时x=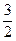
 s;
s;
②如图,若EF=BE,则∠B=∠EFB
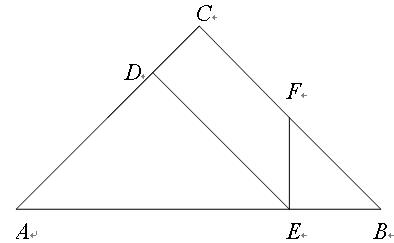
又∵△ADE∽△BEF,∴∠A=∠AED=45°
∴∠ADE=90°,∴AE=3 ,
,
∵动点E的速度为1cm/s
∴此时x=3 s;
s;
③如图,若BF=BE,则∠FEB=∠EFB;
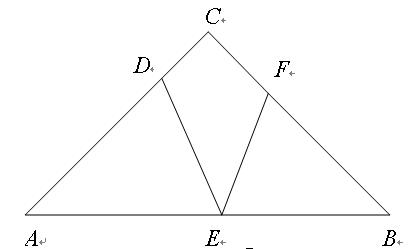
又∵△ADE∽△BEF,∴∠ADE=∠AED
∴AE=AD=3,
∵动点E的速度为1cm/s
∴此时x=3s;
综上所述,当△BEF为等腰三角形时,x的值为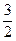
 s或3
s或3 s或3s.
s或3s.
(注:求对一个结论得2分,求对两个结论得4分,求对三个结论得5分)
 ············································································ 2分
············································································ 2分(2)∵在△ABC中,∠C=90°,AC=BC=4.
∴∠A=∠B=45°,AB=4
 ,∴∠ADE+∠AED=135°;
,∴∠ADE+∠AED=135°;又∵∠DEF=45°,∴∠BEF+∠AED=135°,∴∠ADE=∠BEF;
∴△ADE∽△BEF····················································································· 4分
∴
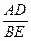 =
=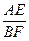 ,
,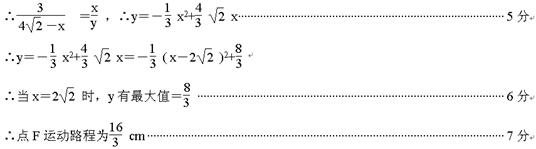
(3)这里有三种情况:
①如图,若EF=BF,则∠B=∠BEF;

又∵△ADE∽△BEF,∴∠A=∠ADE=45°
∴∠AED=90°,∴AE=DE=
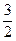
 ,
,∵动点E的速度为1cm/s,∴此时x=
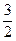
 s;
s;②如图,若EF=BE,则∠B=∠EFB

又∵△ADE∽△BEF,∴∠A=∠AED=45°
∴∠ADE=90°,∴AE=3
 ,
,∵动点E的速度为1cm/s
∴此时x=3
 s;
s;③如图,若BF=BE,则∠FEB=∠EFB;

又∵△ADE∽△BEF,∴∠ADE=∠AED
∴AE=AD=3,
∵动点E的速度为1cm/s
∴此时x=3s;
综上所述,当△BEF为等腰三角形时,x的值为
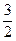
 s或3
s或3 s或3s.
s或3s.(注:求对一个结论得2分,求对两个结论得4分,求对三个结论得5分)
略

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
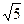 ,这个矩形的长宽各是多少?
,这个矩形的长宽各是多少?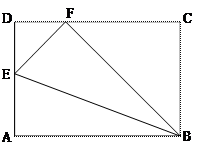

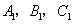 分别是
分别是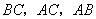 的中点,
的中点,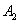 ,
,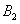 ,
,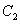 分别是
分别是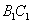 ,
,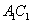 ,
, 的中点
的中点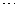 这样延续下去.已知
这样延续下去.已知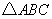 的周长是
的周长是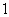 ,
,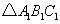 的周长是
的周长是 ,
,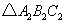 的周长是
的周长是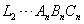 的周长是
的周长是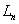 ,则
,则 .(相似三角形、规律探究)
.(相似三角形、规律探究)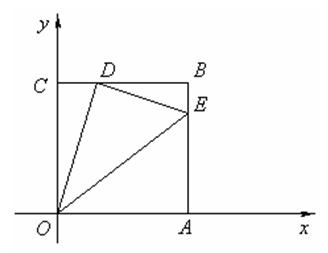
 杆,利用太
杆,利用太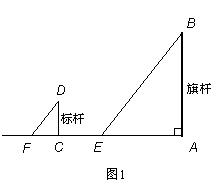
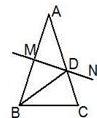
 出必须的工具,设计一个测量方案,以求出旗杆顶端到地面的距离.
出必须的工具,设计一个测量方案,以求出旗杆顶端到地面的距离. 用图中画出示意图,说明需要测量的数据.(注意不能到达底部点N对完成测量任务的影响,不需计算)
用图中画出示意图,说明需要测量的数据.(注意不能到达底部点N对完成测量任务的影响,不需计算)
 ,
, ,△OEF与△OGH组成的图形称为蝶形。
,△OEF与△OGH组成的图形称为蝶形。
 3,CB="5" ,求DE的长.
3,CB="5" ,求DE的长. 1)求证:△ABD为等腰三角形;
1)求证:△ABD为等腰三角形;