题目内容
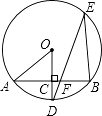
【题目】如图,在Rt△ABC中,∠C=90°,O为AB边上一点,⊙O交AB于E,F两点,BC切⊙O于点D,且CD= ![]() EF=1.
EF=1. 
(1)求证:⊙O与AC相切;
(2)求图中阴影部分的面积.
【答案】
(1)证明:连接OD,过点O作OH⊥AC于点H,
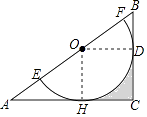
∵BC是⊙O的切线,
∴OD⊥BC.
∵∠C=90°,
∴∠OHC=∠ODC=∠C=90°,
∴四边形OHCD是矩形.
∵CD= ![]() EF,
EF,
∴OH= ![]() EF=OE.
EF=OE.
∵OH⊥AC,
∴AC是⊙O的切线;
(2)解:∵OD= ![]() EF=1,CD=1,∠DOH=90°,
EF=1,CD=1,∠DOH=90°,
∴S阴影=1×1﹣ ![]() =1﹣
=1﹣ ![]() π.
π.
【解析】(1)连接OD,过点O作OH⊥AC于点H,先根据题意得出四边形OHCD是矩形,进而可得出结论;(2)直接根据S阴影=S正方形ODCH﹣S扇形ODH即可得出结论.
【考点精析】掌握扇形面积计算公式是解答本题的根本,需要知道在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目