题目内容
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y= ![]() (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).则点F的坐标是 .
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).则点F的坐标是 . 
【答案】(6, ![]() )
)
【解析】解:∵反比例函数y= ![]() 的图象经过点A,A点的坐标为(4,2), ∴k=2×4=8,
的图象经过点A,A点的坐标为(4,2), ∴k=2×4=8,
∴反比例函数的解析式为y= ![]() ;
;
过点A作AM⊥x轴于点M,过点C作CN⊥x轴于点N,
由题意可知,CN=2AM=4,ON=2OM=8,
∴点C的坐标为C(8,4),
设OB=x,则BC=x,BN=8﹣x,
在Rt△CNB中,x2﹣(8﹣x)2=42 ,
解得:x=5,
∴点B的坐标为B(5,0),
设直线BC的函数表达式为y=ax+b,
∵直线BC过点B(5,0),C(8,4),
∴ ![]() ,解得:
,解得: 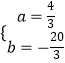 ,
,
∴直线BC的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
根据题意得方程组  ,
,
解此方程组得: ![]() 或
或 ![]() .
.
∵点F在第一象限,
∴点F的坐标为(6, ![]() ).
).
故答案为:(6, ![]() ).
).
将点A的坐标代入到反比例函数的一般形式后求得k值即可确定函数的解析式,过点A作AM⊥x轴于点M,过点C作CN⊥x轴于点N,首先求得点B的坐标,然后求得直线BC的解析式,求得直线和双曲线的交点坐标即可.

【题目】为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
组别 | 分组 | 频数 | 频率 |
1 | 50≤x<60 | 9 | 0.18 |
2 | 60≤x<70 | a | |
3 | 70≤x<80 | 20 | 0.40 |
4 | 80≤x<90 | 0.08 | |
5 | 90≤x≤100 | 2 | b |
合计 |

请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出a、b、x、y的值;
(2)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B)






