题目内容
【题目】如图，甲、乙两人分别从A（1， 
），B（6，0）两点同时出发，点O为坐标原点，甲沿AO方向，乙沿BO方向均以4km/h的速度行驶，th后，甲到达M点，乙到达N点．
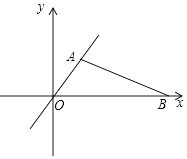
（1）请说明甲、乙两人到达O点前，MN与AB不可能平行；
（2）当t为何值时，△OMN∽△OBA；
（3）甲、乙两人之间的距离为MN的长，设s=MN2 ， 直接写出s与t之间的函数关系式．
【答案】
（1）
解：∵A点的坐标为（1， 
），
∴OA= 
=2；
∵OM=2﹣4t，ON=6﹣4t，
∴当 
= 
时，解得t=0，
∴甲、乙两人到达O点前，只有当t=0时，△OMN∽△OAB，
∴MN与AB不可能平行．
（2）
解：∵甲到达O点的时间为t= 
，乙到达O点的时间为t= 
= 
，
∴甲先到达O点，
∴t= 或t= 时，O、M、N三点不能连接成三角形．
①t＜ 时，
如果△OMN∽△OBA，则有 
= 
，
解得t=2＞ ，
∴△OMN不可能和△OBA相似．
②当 ＜t＜ 时，
∠MON＞∠AOB，
显然△OMN不可能和△OBA相似．
③当t＞ 时，
= 
，
解得t=2＞ ，
∴当t=2时，△OMN∽△OBA．
（3）
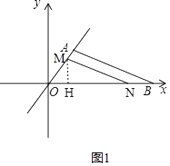
解：①当t≤ 时，如图1，过点M作MH⊥x轴于点H，
，
在Rt△MOH中，
∵∠AOB=60°，
∴MH=OMsin60°=（2﹣4t）× 
= （1﹣2t），
∴OH=OMcos60°=（2﹣4t）× =1﹣2t，
∴NH=（6﹣4t）﹣（1﹣2t）=5﹣2t，
∴s=[ （1﹣2t）]2+（5﹣2t）2
=3（4t2﹣4t+1）+（4t2﹣20t+25）
=16t2﹣32t+28．
②当 ＜t≤ 时，如图2，作MH⊥x轴于点H，
，
在Rt△MOH中，
MH= （4t﹣2）= （2t﹣1），
NH= （4t﹣2）+（6﹣4t）=5﹣2t，
∴s=[ （1﹣2t）]2+（5﹣2t）2=16t2﹣32t+28．
③当t＞ 时，同理可得s=[ （1﹣2t）]2+（5﹣2t）2=16t2﹣32t+28．
综上，可得s=[ （1﹣2t）]2+（5﹣2t）2=16t2﹣32t+28．
【解析】（1）判断出甲、乙两人到达O点前，只有当t=0时，△OMN∽△OAB，即可推得MN与AB不可能平行．（2）根据题意，分三种情况：①t＜ 时；②当 ＜t＜ 时；③当t＞ 时；求出当t为何值时，△OMN∽△OBA．（3）根据题意，分三种情况：①t≤ 时；②当 ＜t≤ 时；③当t＞ 时；写出s与t之间的函数关系式即可．
【考点精析】关于本题考查的二次函数的图象和二次函数的性质，需要了解二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．
