题目内容
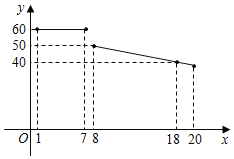
【题目】某水果超市经销一种进价为18元/kg的水果，根据以前的销售经验，该种水果的最佳销售期为20天，销售人员整理出这种水果的销售单价y（元/kg）与第x天（1≤x≤20）的函数图象如图所示，而第x天（1≤x≤20）的销售量m（kg）是x的一次函数，满足下表：
x（天） | 1 | 2 | 3 | … |
m（kg） | 20 | 24 | 28 | … |
（1）请分别写出销售单价y（元/kg）与x（天）之间及销售量m（kg）是x（天）的之间的函数关系式
（2）求在销售的第几天时，当天的利润最大，最大利润是多少？
（3）请求出试销的20天中当天的销售利润不低于1680元的天数．
【答案】（1）y＝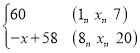
，m＝4x+16（0≤x≤20，且x为整数）；（2）在销售的第18天时，当天的利润最大，最大利润是1936元；（3）试销的20天中当天的销售利润不低于1680元的有13天
【解析】
(1)利用待定系数法求解可得；
(2)设当天的总利润为w，分1≤x≤7和8≤x≤20两种情况，根据“总利润=每千克利润×日销售量”列出函数解析式，再依据一次函数和二次函数的性质分别求解可得；
(3)在两种情况下，分别求出w≥1680时对应的x的范围，从而得出答案．
(1)当1≤x≤7时，y=60；
当8≤x≤20时，设y=kx+b，
将(8，50)、(18，40)代入得
，
解得
，
∴
；
综上，y=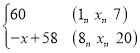
设
，
将(1，20)、(2，24)代入得
，
解得
，
则
(0≤x≤20，且x为整数)；
(2)设当天的总利润为w，
当
时，
，
则
时，w取得最大值，最大值为1848元；
当
时，
，
∴当x=18时，w取得最大值，最大利润为1936元；
综上，在销售的第18天时，当天的利润最大，最大利润是1936元；
(3)当时，
，
解得
，
∴此时满足条件的天数为第6、7这2天；
当时，
，
解得
，
又∵
，
∴
，
∴此时满足条件的天数有11天；
综上，试销的20天中当天的销售利润不低于1680元的有13天．
