Question

【题目】如图，在中，，点在边上，点在边上，且是的直径，的平分线与相交于点.

（1）证明：直线是的切线；

（2）连接，若，，求边的长.

Answer 1

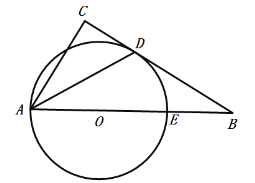
【答案】（1）见解析；（2）12

【解析】

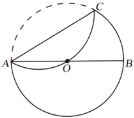
（1）连接OD，AD是∠CAB的平分线，以及OA=DO，推出∠CAD=∠ODA,进而得出OD∥AC,最后根据∠C=90°可得出结论；
（2）因为∠B=30°，所以∠CAB=60°，结合（1）可得AC∥OD，证明△ODE是等边三角形，进而求出OA的长．再在Rt△BOD中，利用含30°直角三角形的性质求出BO的长，从而得出结论．

解：（1）证明：连接

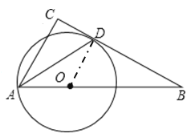
平分∠CAB，

．

在中，，

．

．

∴AC∥OD．

中，，

，直线为圆的切线；

（2）解：如图，

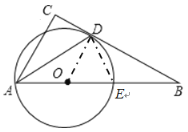
中，，,

∴．

由（1）可得：AC∥OD，

，

为等边三角形，，

．

由（1）可得，

又，

在中，．

．