ЬтФПФкШн
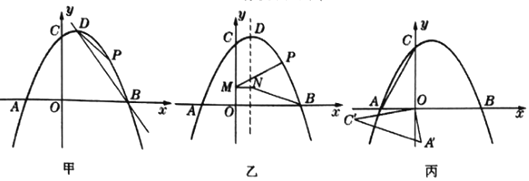
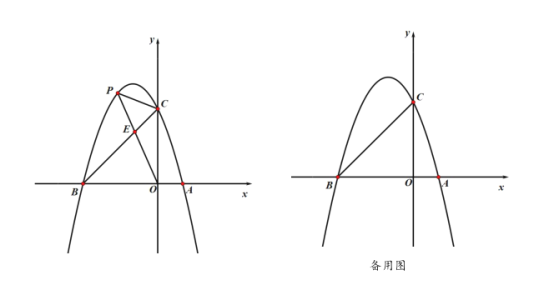
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+2НЛxжсгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉСНЕуЃЌНЛyжсгкЕуCЃЌгыЙ§ЕуCЧвЦНаагкxжсЕФжБЯпНЛгкСэвЛЕуDЃЌЕуPЪЧХзЮяЯпЩЯвЛЖЏЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНМАЕуDзјБъЃЛ
ЃЈ2ЃЉЕуEдкxжсЩЯЃЌШєвдAЃЌEЃЌDЃЌPЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧѓДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЙ§ЕуPзїжБЯпCDЕФДЙЯпЃЌДЙзуЮЊQЃЌШєНЋЁїCPQбиCPЗелЃЌЕуQЕФЖдгІЕуЮЊQЁфЃЎЪЧЗёДцдкЕуPЃЌЪЙQЁфЧЁКУТфдкxжсЩЯЃПШєДцдкЃЌЧѓГіДЫЪБЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌЕуDзјБъЮЊЃЈ3ЃЌ2ЃЉЃЈ2ЃЉP1ЃЈ0ЃЌ2ЃЉЃЛP2ЃЈ
ЃЌЕуDзјБъЮЊЃЈ3ЃЌ2ЃЉЃЈ2ЃЉP1ЃЈ0ЃЌ2ЃЉЃЛP2ЃЈ![]() ЃЌЉ2ЃЉЃЛP3ЃЈ
ЃЌЉ2ЃЉЃЛP3ЃЈ![]() ЃЌЉ2ЃЉЃЈ3ЃЉДцдкЃЌЃЈ
ЃЌЉ2ЃЉЃЈ3ЃЉДцдкЃЌЃЈ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
НтЃКЃЈ1ЃЉЁпХзЮяЯпy=ax2+bx+2ОЙ§AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉСНЕуЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК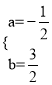 ЃЎ
ЃЎ
ЁрХзЮяЯпНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
ЕБy=2ЪБЃЌ![]() ЃЌНтЕУЃКx1=3ЃЌx2=0ЃЈЩсШЅЃЉЃЎ
ЃЌНтЕУЃКx1=3ЃЌx2=0ЃЈЩсШЅЃЉЃЎ
ЁрЕуDзјБъЮЊЃЈ3ЃЌ2ЃЉЃЎ
ЃЈ2ЃЉAЃЌEСНЕуЖМдкxжсЩЯЃЌAEгаСНжжПЩФмЃК
ЂйЕБAEЮЊвЛБпЪБЃЌAEЁЮPDЃЌЁрP1ЃЈ0ЃЌ2ЃЉЃЎ
ЂкЕБAEЮЊЖдНЧЯпЪБЃЌИљОнЦНааЫФБпаЮЖдЖЅЕуЕНСэвЛЬѕЖдНЧЯпОрРыЯрЕШЃЌПЩжЊPЕуЁЂDЕуЕНжБЯпAEЃЈМДxжсЃЉЕФОрРыЯрЕШЃЌЁрPЕуЕФзнзјБъЮЊЉ2ЃЎ
ДњШыХзЮяЯпЕФНтЮіЪНЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЎ
ЃЎ
ЁрPЕуЕФзјБъЮЊЃЈ![]() ЃЌЉ2ЃЉЃЌЃЈ
ЃЌЉ2ЃЉЃЌЃЈ![]() ЃЌЉ2ЃЉЃЎ
ЃЌЉ2ЃЉЃЎ
злЩЯЫљЪіЃКP1ЃЈ0ЃЌ2ЃЉЃЛP2ЃЈ![]() ЃЌЉ2ЃЉЃЛP3ЃЈ
ЃЌЉ2ЃЉЃЛP3ЃЈ![]() ЃЌЉ2ЃЉЃЎ
ЃЌЉ2ЃЉЃЎ
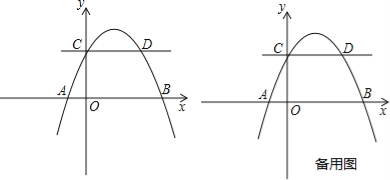
ЃЈ3ЃЉДцдкТњзуЬѕМўЕФЕуPЃЌЯдШЛЕуPдкжБЯпCDЯТЗНЃЎ
ЩшжБЯпPQНЛxжсгкFЃЌЕуPЕФзјБъЮЊЃЈ![]() ЃЉЃЌ
ЃЉЃЌ
ЂйЕБPЕудкyжсгвВрЪБЃЈШчЭМ1ЃЉЃЌCQ=aЃЌ
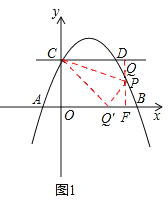
PQ=![]() ЃЎ
ЃЎ
гжЁпЁЯCQЁфO+ЁЯFQЁфP=90ЁуЃЌЁЯCOQЁф=ЁЯQЁфFP=90ЁуЃЌ
ЁрЁЯFQЁфP=ЁЯOCQЁфЃЌЁрЁїCOQЁфЁзЁїQЁфFPЃЌ
Ёр![]() ЃЌМД
ЃЌМД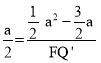 ЃЌНтЕУF QЁф=aЉ3
ЃЌНтЕУF QЁф=aЉ3
ЁрOQЁф=OFЉF QЁф=aЉЃЈaЉ3ЃЉ=3ЃЌ
![]() ЃЎ
ЃЎ
ДЫЪБa=![]() ЃЌЕуPЕФзјБъЮЊЃЈ
ЃЌЕуPЕФзјБъЮЊЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
ЂкЕБPЕудкyжсзѓВрЪБЃЈШчЭМ2ЃЉДЫЪБaЃМ0ЃЌЃЌ![]() ЃМ0ЃЌCQ=ЉaЃЌЃЈЮоЭМЃЉ
ЃМ0ЃЌCQ=ЉaЃЌЃЈЮоЭМЃЉ
PQ=![]() ЃЎ
ЃЎ
гжЁпЁЯCQЁфO+ЁЯFQЁфP=90ЁуЃЌЁЯCQЁфO+ЁЯOCQЁф=90ЁуЃЌ
ЁрЁЯFQЁфP=ЁЯOCQЁфЃЌЁЯCOQЁф=ЁЯQЁфFP=90ЁуЃЎ
ЁрЁїCOQЁфЁзЁїQЁфFPЃЎ
Ёр![]() ЃЌМД
ЃЌМД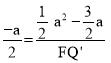 ЃЌНтЕУF QЁф=3ЉaЃЎ
ЃЌНтЕУF QЁф=3ЉaЃЎ
ЁрOQЁф=3ЃЌ![]() ЃЎ
ЃЎ
ДЫЪБa=Љ![]() ЃЌЕуPЕФзјБъЮЊЃЈ
ЃЌЕуPЕФзјБъЮЊЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуPзјБъЮЊЃЈ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉгУД§ЖЈЯЕЪ§ЗЈПЩЕУГіХзЮяЯпЕФНтЮіЪНЃЌСюy=2ПЩЕУГіЕуDЕФзјБъЃЎ
ЃЈ2ЃЉЗжСНжжЧщПіНјааЬжТлЃЌЂйЕБAEЮЊвЛБпЪБЃЌAEЁЮPDЃЌЂкЕБAEЮЊЖдНЧЯпЪБЃЌИљОнЦНааЫФБпаЮЖдЖЅЕуЕНСэвЛЬѕЖдНЧЯпОрРыЯрЕШЃЌЧѓНтЕуPзјБъЃЎ
ЃЈ3ЃЉНсКЯЭМаЮПЩХаЖЯГіЕуPдкжБЯпCDЯТЗНЃЌЩшЕуPЕФзјБъЮЊЃЈ![]() ЃЉЃЌЗжЧщПіЬжТлЃЌЂйЕБPЕудкyжсгвВрЪБЃЌЂкЕБPЕудкyжсзѓВрЪБЃЌдЫгУНтжБНЧШ§НЧаЮМАЯрЫЦШ§НЧаЮЕФаджЪНјааЧѓНтМДПЩЃЎ
ЃЉЃЌЗжЧщПіЬжТлЃЌЂйЕБPЕудкyжсгвВрЪБЃЌЂкЕБPЕудкyжсзѓВрЪБЃЌдЫгУНтжБНЧШ§НЧаЮМАЯрЫЦШ§НЧаЮЕФаджЪНјааЧѓНтМДПЩЃЎ

 дФЖСПьГЕЯЕСаД№АИ
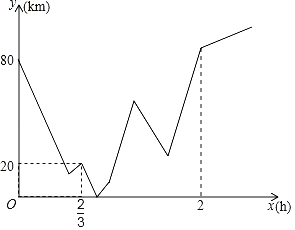
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁП![]() ЃЌ
ЃЌ![]() СНЕиЯрОр
СНЕиЯрОр![]() ЃЌМзЁЂввСНШЫЖМгЩ
ЃЌМзЁЂввСНШЫЖМгЩ![]() ЕиШЅ
ЕиШЅ![]() ЕиЃЌМзЦяздааГЕЃЌЦНОљЫйЖШЮЊ
ЕиЃЌМзЦяздааГЕЃЌЦНОљЫйЖШЮЊ![]() ЃЛввГЫЦћГЕЃЌЦНОљЫйЖШЮЊ
ЃЛввГЫЦћГЕЃЌЦНОљЫйЖШЮЊ![]() ЃЌЧвБШМзЭэ
ЃЌЧвБШМзЭэ![]() ГіЗЂ.ЩшМзЕФЦяааЪБМфЮЊ
ГіЗЂ.ЩшМзЕФЦяааЪБМфЮЊ![]()
![]() ЃЎ
ЃЎ
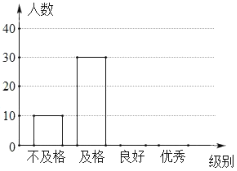
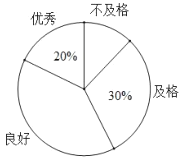
ЃЈ1ЃЉИљОнЬтвтЃЌЬюаДБэИёЃК
ЪБМф гы | 0.5 | 1.8 | |
Мзгы | 5 | 20 | |
ввгы | 0 | 12 |
ЃЈ2ЃЉЩшМзЃЌввСНШЫгы![]() ЕиЕФОрРыЮЊ
ЕиЕФОрРыЮЊ![]() КЭ
КЭ![]() .аДГі
.аДГі![]() ЃЌ
ЃЌ![]() Йигк
Йигк![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ3ЃЉЩшМзЃЌввСНШЫжЎМфЕФОрРыЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.