ЬтФПФкШн
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃЌЭъГЩЃЈ1ЃЉЁЂЃЈ2ЃЉЬтЃЎ
Ъ§бЇПЮЩЯЃЌРЯЪІГіЪОСЫетбљвЛЕРЬтЃК![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЕФбгГЄЯпЩЯЃЌЧв
ЕФбгГЄЯпЩЯЃЌЧв![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ДЙзуЮЊ
ДЙзуЮЊ![]() ЃЌЬНОПЯпЖЮ
ЃЌЬНОПЯпЖЮ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
ЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
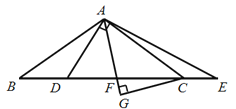
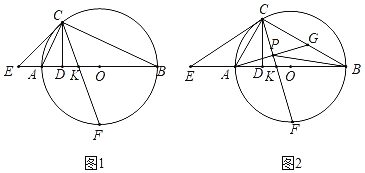
ЭЌбЇУЧОЙ§ЫМПМКѓЃЌНЛСїСЫздМКЕФЯыЗЈЃК
аЁУїЃКЁАЭЈЙ§ЙлВьКЭЖШСПЃЌЗЂЯж![]() гы
гы![]() ЯрЕШЃЎЁБ
ЯрЕШЃЎЁБ
аЁЧПЃКЁАЭЈЙ§ЙлВьКЭЖШСПЃЌЗЂЯжЭМжаЛЙгаЦфЫќЯрЕШЯпЖЮЃЎЁБ
аЁЮАЃКЁАЭЈЙ§ЙЙдьШЋЕШШ§НЧаЮЃЌОЙ§НјвЛВНЭЦРэЃЌПЩвдЕУЕНЯпЖЮ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃЎЁБ
ЕФЪ§СПЙиЯЕЃЎЁБ
ЁЁ
РЯЪІЃКЁАДЫЬтЛЙгаЦфЫќНтЗЈЃЌЭЌбЇУЧПЮКѓПЩвдМЬајЬНОПЃЌЛЅЯрНЛСїЃЎЁБ
ЁЁ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЬНОПЯпЖЮ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃЈгУКЌ
ЕФЪ§СПЙиЯЕЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉЃЌВЂжЄУїЃЎ
ЕФДњЪ§ЪНБэЪОЃЉЃЌВЂжЄУїЃЎ
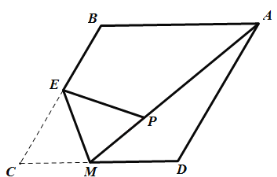
ЁОД№АИЁПЃЈ1ЃЉМћНтЮі ЃЈ2ЃЉ![]() ЃЌРэгЩМћНтЮі
ЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЯШИљОнЕШбќШ§НЧаЮЕФаджЪЕУГі![]() ЃЌШЛКѓРћгУ
ЃЌШЛКѓРћгУ![]() ЃЌ
ЃЌ![]() КЭЕШСПДњЛЛМДПЩжЄУїНсТлЃЛ
КЭЕШСПДњЛЛМДПЩжЄУїНсТлЃЛ
ЃЈ2ЃЉЙ§Еу![]() зї
зї![]() ДЙзуЮЊ
ДЙзуЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ДЙзуЮЊ
ДЙзуЮЊ![]() ЃЌЯШРћгУНЧЦНЗжЯпЕФЖЈвхКЭЕШбќШ§НЧаЮЕФЖЈвхМАШ§НЧаЮФкНЧКЭЖЈРэЕУГі
ЃЌЯШРћгУНЧЦНЗжЯпЕФЖЈвхКЭЕШбќШ§НЧаЮЕФЖЈвхМАШ§НЧаЮФкНЧКЭЖЈРэЕУГі![]() ЃЌдђ
ЃЌдђ![]() ЃЌдйЭЈЙ§ЕШСПДњЛЛЕУГі
ЃЌдйЭЈЙ§ЕШСПДњЛЛЕУГі![]() ЃЌдђ
ЃЌдђ![]() ЃЌНјЖјга
ЃЌНјЖјга![]() ЃЌШЛКѓжЄУї
ЃЌШЛКѓжЄУї![]() ЃЌдђга
ЃЌдђга![]() ЃЌдйжЄУї
ЃЌдйжЄУї![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌдђ
ЃЌдђ![]() ЃЌДгЖјПЩЕУГі
ЃЌДгЖјПЩЕУГі![]() ЃЎ
ЃЎ
ЃЈ1ЃЉжЄУїЃК![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЃЎ
ЃЎ
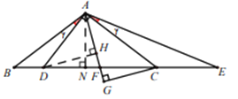
ЃЈ2ЃЉ![]() ЃЌРэгЩШчЯТЃК
ЃЌРэгЩШчЯТЃК
ШчЭМЃЌЙ§Еу![]() зї
зї![]() ДЙзуЮЊ
ДЙзуЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ДЙзуЮЊ
ДЙзуЮЊ![]() ЃЌ
ЃЌ
дђ![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
гЩЃЈ1ЃЉ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЃЎ
ЃЎ
![]() ЃЎ
ЃЎ
![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ![]()
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ
 ЃЎ
ЃЎ
![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ

ЁОЬтФПЁПФГаЃЮЊСЫНтЦпФъМЖФаЩњЁАЬјЩўЁБГЩМЈЕФЧщПіЃЌЫцЛњбЁШЁИУФъМЖВПЗжФаЩњНјааВтЪдЃЎвдЯТЪЧИљОнВтЪдГЩМЈЛцжЦЕФЭГМЦЭМБэЕФвЛВПЗжЃЎ
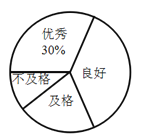
ГЩМЈЕШМЖ | ЦЕЪ§ЃЈШЫЃЉ | ЦЕТЪ |
гХау | ||
СМКУ | ||
МАИё | 10 | 0ЃЎ2 |
ВЛМАИё | 0ЃЎ1 |
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБЛВтЪдФаЩњжаЃЌГЩМЈЕШМЖЮЊЁАгХауЁБЕФФаЩњШЫЪ§еМБЛВтЪдФаЩњзмШЫЪ§ЕФАйЗжБШЮЊ________%ЃЌГЩМЈЕШМЖЮЊЁАМАИёЁБЕФФаЩњШЫЪ§ЮЊ________ШЫЃЛ
ЃЈ2ЃЉБЛВтЪдФаЩњЕФзмШЫЪ§ЮЊ________ШЫЃЌГЩМЈЕШМЖЮЊЁАВЛМАИёЁБЕФФаЩњШЫЪ§________ШЫЃЛ
ЃЈ3ЃЉШєИУаЃЦпФъМЖЙВга570УћФаЩњЃЌИљОнЕїВщНсЙћЃЌЙРМЦИУаЃЦпФъМЖФаЩњГЩМЈЕШМЖЮЊЁАСМКУЁБЕФбЇЩњШЫЪ§ЃЎ