题目内容
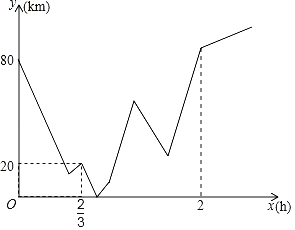
【题目】A、B两地之间有一修理厂C,一日小海和王陆分别从A、B两地同时出发相向而行,王陆开车,小海骑摩托.二人相遇时小海的摩托车突然出故障无法前行,王陆决定将小海和摩托车一起送回到修理厂C后再继续按原路前行,王陆到达A地后立即返回B地,到B地后不再继续前行,等待小海前来(装载摩托车时间和掉头时间忽略不计),整个行驶过程中王陆速度不变,而小海在修理厂花了十分钟修好摩托车,为了赶时间,提速![]() 前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有_____km.
前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有_____km.
【答案】14
【解析】
从![]() 时,
时,![]() 得
得![]() 、
、![]() 两地距离为
两地距离为![]() ,再从
,再从![]() ,
,![]() 得,第一次相遇点与
得,第一次相遇点与![]() 点距离为
点距离为![]() ,根据题意与函数图象知,当
,根据题意与函数图象知,当![]() 时,王陆回到了
时,王陆回到了![]() 点,进而求得王陆的速度,再根据相遇问题求出两人的速度和,进而得小海的速度,设把摩托车送回到修理厂
点,进而求得王陆的速度,再根据相遇问题求出两人的速度和,进而得小海的速度,设把摩托车送回到修理厂![]() 后,再过
后,再过![]() ,两人第二次相遇,根据追及问题列出方程求得
,两人第二次相遇,根据追及问题列出方程求得![]() ,进而求得第二次相遇时,他们距
,进而求得第二次相遇时,他们距![]() 地的距离,即可求得结果.
地的距离,即可求得结果.
解:从函数图象可知,∵x=0h时,y=80km,
∴AB=80km,
设两人第一次相遇地点为D地,
∵x=![]() h,y=20km,
h,y=20km,
∴BD﹣BC=20÷2=10(km),
由函数图象可知,当时间x=2h时,王陆回到了B地,
∴王陆的速度为:(80×2+10×2)÷2=90(km/h),
∴小海原来的速度为:80÷![]() ﹣90=30(km/h),
﹣90=30(km/h),
小海后来的速度为:30×(1+![]() )=40(km/h),
)=40(km/h),
设把摩托车送回到修理厂C后,再过ah,两人第二次相遇,则
90a=[30×![]() +10]×2+40(a﹣﹣
+10]×2+40(a﹣﹣![]() ),
),
∴a=![]() ,
,
∴当王陆第二次与小海在行驶中相遇时,小海离目的地B的距离为:
80﹣[30×![]() +10+40(a﹣﹣
+10+40(a﹣﹣![]() )]=14.
)]=14.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案