ƒøƒ⁄»ð
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„![]() Œ™◊¯±Í‘≠µ„£¨≈◊ŒÔœþ
Œ™◊¯±Í‘≠µ„£¨≈◊ŒÔœþ![]() ”Î
”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨µ„
£¨µ„![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨µ„
£¨µ„![]() ‘⁄µ⁄∂˛œÛœÞµƒ≈◊ŒÔœþ…œ£¨¡¨Ω”
‘⁄µ⁄∂˛œÛœÞµƒ≈◊ŒÔœþ…œ£¨¡¨Ω”![]() £¨œþ∂Œ
£¨œþ∂Œ![]() Ωªœþ∂Œ
Ωªœþ∂Œ![]() ”⁄µ„
”⁄µ„![]() £Æ
£Æ
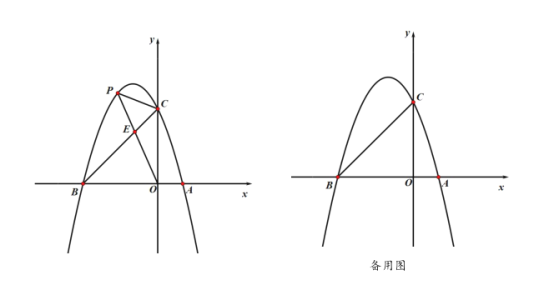
£®1£©«Û≈◊ŒÔœþµƒ±Ì¥Ô Ω£ª
£®2£©»Ù![]() µƒ√ʪ˝Œ™
µƒ√ʪ˝Œ™![]() £¨
£¨![]() µƒ√ʪ˝Œ™
µƒ√ʪ˝Œ™![]() µ±
µ±![]() ±£¨«Ûµ„
±£¨«Ûµ„![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
£®3£©“—÷™µ„![]() πÿ”⁄≈◊ŒÔœþ∂‘≥∆÷·µƒ∂‘≥∆µ„Œ™µ„
πÿ”⁄≈◊ŒÔœþ∂‘≥∆÷·µƒ∂‘≥∆µ„Œ™µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨µ„
£¨µ„![]() ‘⁄
‘⁄![]() ÷·…œ£¨µ±
÷·…œ£¨µ±![]() ±£¨
±£¨
¢Ÿ«Û¬˙◊„Ãıº˛µƒÀ˘”–µ„![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
¢⁄µ±µ„![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() …œ ±£¨µ„
…œ ±£¨µ„![]() «œþ∂Œ
«œþ∂Œ![]() Õ‚“ªµ„£¨
Õ‚“ªµ„£¨![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨Ω´œþ∂Œ
£¨Ω´œþ∂Œ![]() »∆◊≈µ„
»∆◊≈µ„![]() À≥ ±’Ζ˝◊™
À≥ ±’Ζ˝◊™![]() £¨µ√µΩœþ∂Œ
£¨µ√µΩœþ∂Œ![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨÷±Ω”–¥≥ˆœþ∂Œ
£¨÷±Ω”–¥≥ˆœþ∂Œ![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£©![]() ªÚ
ªÚ![]() £ª£®3£©¢Ÿ
£ª£®3£©¢Ÿ![]() ªÚ
ªÚ![]() £ª¢⁄
£ª¢⁄![]()
°æΩ‚Œˆ°ø
£®1£©Ω´µ„A°¢B◊¯±Í¥˙»ÎΩ‚Œˆ ΩΩ‚¥º¥ø…£ª
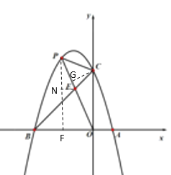
£®2£©œ»«Û≥ˆµ„Cµƒ◊¯±ÍŒ™£®0,3£©£¨π˝µ„C◊˜CG°ÕOP”⁄G£¨∏˘æð![]() £¨
£¨![]() £¨
£¨![]() µ√µΩ
µ√µΩ![]() £¨π˝µ„P◊˜PF°Õx÷·”⁄F£¨π˝µ„E◊˜EN°ÕPF”⁄N£¨µ√µΩ
£¨π˝µ„P◊˜PF°Õx÷·”⁄F£¨π˝µ„E◊˜EN°ÕPF”⁄N£¨µ√µΩ![]() £¨…˵„Pµƒ◊¯±ÍŒ™£®a£¨
£¨…˵„Pµƒ◊¯±ÍŒ™£®a£¨![]() £©£¨«Û≥ˆ÷±œþBCµƒΩ‚Œˆ ΩŒ™y=x+3£¨µ√µΩE£®
£©£¨«Û≥ˆ÷±œþBCµƒΩ‚Œˆ ΩŒ™y=x+3£¨µ√µΩE£®![]() £¨
£¨![]() +3£©£¨∏˘æð2PF=5PNµ√µΩ5(
+3£©£¨∏˘æð2PF=5PNµ√µΩ5(![]() -
-![]() -3)=2(
-3)=2(![]() )£¨«Û≥ˆx÷µº¥ø…µ√µΩµ„Pµƒ◊¯±Í£ª
)£¨«Û≥ˆx÷µº¥ø…µ√µΩµ„Pµƒ◊¯±Í£ª
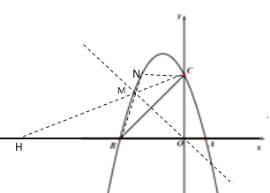
£®3£©¢Ÿœ»«Û≥ˆ≈◊ŒÔœþµƒ∂‘≥∆÷· «÷±œþx=-1£¨µ√µΩN£®-2,3£©£¨«Û≥ˆ÷±œþBNµƒΩ‚Œˆ ΩŒ™y=3x+9£¨∑÷¡Ω÷÷«Èøˆ£∫µ±µ„H‘⁄OB÷ƺ‰ ±£¨”…![]() £¨µ√µΩBN°ŒCH£¨µ√µΩ÷±œþCHµƒΩ‚Œˆ ΩŒ™y=3x+3£¨º¥ø…«Û≥ˆµ„Hµƒ◊¯±ÍŒ™£®-1,0£©£ªµ±µ„H‘⁄µ„B◊Û≤ý ±£¨CHΩªBN”⁄M£¨◊˜÷±œþOM£¨”…
£¨µ√µΩBN°ŒCH£¨µ√µΩ÷±œþCHµƒΩ‚Œˆ ΩŒ™y=3x+3£¨º¥ø…«Û≥ˆµ„Hµƒ◊¯±ÍŒ™£®-1,0£©£ªµ±µ„H‘⁄µ„B◊Û≤ý ±£¨CHΩªBN”⁄M£¨◊˜÷±œþOM£¨”…![]() µ√µΩBM=MC£¨π OM «BCµƒ¥π÷±∆Ω∑÷œþ£¨«Û≥ˆΩªµ„Mµƒ◊¯±ÍŒ™£®-
µ√µΩBM=MC£¨π OM «BCµƒ¥π÷±∆Ω∑÷œþ£¨«Û≥ˆΩªµ„Mµƒ◊¯±ÍŒ™£®-![]() £¨
£¨![]() £©£¨‘Ÿ«Û≥ˆ÷±œþCMµƒΩ‚Œˆ ΩŒ™y=
£©£¨‘Ÿ«Û≥ˆ÷±œþCMµƒΩ‚Œˆ ΩŒ™y=![]() x+3£¨º¥ø…µ√µΩµ„Hµƒ◊¯±ÍŒ™£®-9,0£©£ª¢⁄»ÁÕº1£¨µ±µ„Q‘⁄x÷·œ¬∑Ω«“MH°Õx÷· ±£¨MH◊Ó–°£¨◊˜QG°Õx÷·£¨π˝µ„M◊˜MF°ÕQG”⁄F£¨‘ÚÀƒ±þ–ŒMHGF «æÿ–Œ£¨÷§√˜°˜BQG°’°˜QMF£¨µ√µΩFM=GQ£¨BG=FQ£¨¿˚”√π¥π…∂®¿Ì«Û≥ˆGQ=GH=
x+3£¨º¥ø…µ√µΩµ„Hµƒ◊¯±ÍŒ™£®-9,0£©£ª¢⁄»ÁÕº1£¨µ±µ„Q‘⁄x÷·œ¬∑Ω«“MH°Õx÷· ±£¨MH◊Ó–°£¨◊˜QG°Õx÷·£¨π˝µ„M◊˜MF°ÕQG”⁄F£¨‘ÚÀƒ±þ–ŒMHGF «æÿ–Œ£¨÷§√˜°˜BQG°’°˜QMF£¨µ√µΩFM=GQ£¨BG=FQ£¨¿˚”√π¥π…∂®¿Ì«Û≥ˆGQ=GH=![]() £¨µ√µΩMH=FG=BG-FG=
£¨µ√µΩMH=FG=BG-FG=![]() £ª»ÁÕº2£¨µ±µ„Q‘⁄x÷·…œ∑Ω£¨«“MH°Õx÷· ±£¨MH◊Ó¥Û£¨π˝µ„Q◊˜QG°Õx÷·£¨QF°ÕMH”⁄F£¨‘ÚÀƒ±þ–ŒHGQF «æÿ–Œ£¨Õ¨¿Ì£∫°˜BGQ°’°˜MFQ£¨µ√µΩQG=FQ=HG£¨BG=MF£¨¿˚”√π¥π…∂®¿Ì«Û≥ˆGQ=GH=
£ª»ÁÕº2£¨µ±µ„Q‘⁄x÷·…œ∑Ω£¨«“MH°Õx÷· ±£¨MH◊Ó¥Û£¨π˝µ„Q◊˜QG°Õx÷·£¨QF°ÕMH”⁄F£¨‘ÚÀƒ±þ–ŒHGQF «æÿ–Œ£¨Õ¨¿Ì£∫°˜BGQ°’°˜MFQ£¨µ√µΩQG=FQ=HG£¨BG=MF£¨¿˚”√π¥π…∂®¿Ì«Û≥ˆGQ=GH=![]() £¨µ√µΩMH=BG+FH=
£¨µ√µΩMH=BG+FH=![]() £¨º¥ø…µ√µΩMHµƒ»°÷µ∑∂Œß.
£¨º¥ø…µ√µΩMHµƒ»°÷µ∑∂Œß.
£®1£©Ω´µ„A°¢Bµƒ◊¯±Í¥˙»Î![]() ÷–£¨µ√
÷–£¨µ√
![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
°ý≈◊ŒÔœþµƒ±Ì¥Ô ΩŒ™![]() £ª
£ª
£®2£©µ±x=0 ±£¨y=3£¨°ýµ„Cµƒ◊¯±ÍŒ™£®0,3£©£¨
π˝µ„C◊˜CG°ÕOP”⁄G£¨
°þ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
π˝µ„P◊˜PF°Õx÷·”⁄F£¨π˝µ„E◊˜EN°ÕPF”⁄N£¨
°ýEN°ŒOF£¨
°ý![]() ,
,
…˵„Pµƒ◊¯±ÍŒ™£®a£¨![]() £©£¨
£©£¨
°ýOF=-a£¨EN=-![]() £¨
£¨
°ýµ„Eµƒ∫·◊¯±ÍŒ™![]() £¨
£¨
°þB£®3,0£©£¨C£®0,3£©£¨
°ý÷±œþBCµƒΩ‚Œˆ ΩŒ™y=x+3£¨
µ±x=![]() ±£¨y=
±£¨y=![]() +3£¨
+3£¨
°ýE£®![]() £¨
£¨![]() +3£©£¨
+3£©£¨
°þ2PF=5PN£¨
°ý5(![]() -
-![]() -3)=2(
-3)=2(![]() ),
),
Ω‚µ√![]() £¨
£¨![]() £¨
£¨
°ýµ„Pµƒ◊¯±ÍŒ™£®-1,4£©ªÚ£®-2,3£©£ª
£®3£©¢Ÿ°þ![]()
![]() £¨
£¨
°ý≈◊ŒÔœþµƒ∂‘≥∆÷· «÷±œþx=-1£¨
°þµ„![]() πÿ”⁄≈◊ŒÔœþ∂‘≥∆÷·µƒ∂‘≥∆µ„Œ™µ„
πÿ”⁄≈◊ŒÔœþ∂‘≥∆÷·µƒ∂‘≥∆µ„Œ™µ„![]() £¨C£®0,3£©£¨
£¨C£®0,3£©£¨
°ýN£®-2,3£©£¨
…Ë÷±œþBNµƒΩ‚Œˆ ΩŒ™y=kx+b£¨
°ý![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
°ý÷±œþBNµƒΩ‚Œˆ ΩŒ™y=3x+9£¨
µ±µ„H‘⁄OB÷ƺ‰ ±£¨»ÁÕº£¨
°þ![]() £¨
£¨
°ýBN°ŒCH£¨
…Ë÷±œþCHµƒΩ‚Œˆ ΩŒ™y=3x+m£¨Ω´µ„Cµƒ◊¯±Í¥˙»Î£¨µ√m=3,
°ý÷±œþCHµƒΩ‚Œˆ ΩŒ™y=3x+3£¨
µ±y=0 ±£¨µ√x=-1£¨
°ýµ„Hµƒ◊¯±ÍŒ™£®-1,0£©£ª
µ±µ„H‘⁄µ„B◊Û≤ý ±£¨»ÁÕº£¨CHΩªBN”⁄M£¨◊˜÷±œþOM£¨
°þ![]() £¨
£¨
°ýBM=MC£¨
°þOB=OC£¨
°ýOM «BCµƒ¥π÷±∆Ω∑÷œþ£¨
°ý÷±œþOMµƒΩ‚Œˆ ΩŒ™y=-x£¨
Ω‚∑Ω≥Ã◊È![]() £¨µ√
£¨µ√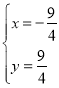 £¨
£¨
°ýµ„Mµƒ◊¯±ÍŒ™£®-![]() £¨
£¨![]() £©£¨
£©£¨
…Ë÷±œþCMµƒΩ‚Œˆ ΩŒ™y=cx+n£¨
°ý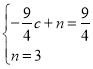 £¨°ý
£¨°ý![]() £¨
£¨
°ý÷±œþCMµƒΩ‚Œˆ ΩŒ™y=![]() x+3£¨
x+3£¨
µ±y=0 ±x=-9£¨°ýµ„Hµƒ◊¯±ÍŒ™£®-9,0£©£¨
◊€…œ£¨µ±![]() ±£¨µ„Hµƒ◊¯±ÍŒ™£®-1,0£©ªÚ£®-9£¨0£©£ª
±£¨µ„Hµƒ◊¯±ÍŒ™£®-1,0£©ªÚ£®-9£¨0£©£ª
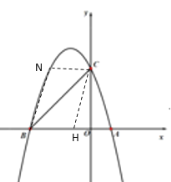
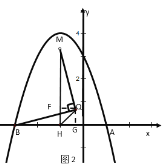
¢⁄»ÁÕº1£¨µ±µ„Q‘⁄x÷·œ¬∑Ω«“MH°Õx÷· ±£¨MH◊Ó–°£¨◊˜QG°Õx÷·£¨π˝µ„M◊˜MF°ÕQG”⁄F£¨‘ÚÀƒ±þ–ŒMHGF «æÿ–Œ£¨
°ýFM=GH£¨FG=MH£¨
°þ°œBQM=°œF=90°„£¨
°ý°œBQG+°œFQM=°œFMQ+°œFQM=90°„£¨
°ý°œBQG=°œFMQ£¨
°þ°œBGQ=°œF£¨BQ=MQ£¨
°ý°˜BQG°’°˜QMF£¨
°ýFM=GQ£¨BG=FQ£¨
°ýGQ=FM=GH£¨
°þQH=1£¨
°ýGQ=GH=![]() £¨
£¨
°ý MH=FG=BG-FG=![]() £ª
£ª
»ÁÕº2£¨µ±µ„Q‘⁄x÷·…œ∑Ω£¨«“MH°Õx÷· ±£¨MH◊Ó¥Û£¨π˝µ„Q◊˜QG°Õx÷·£¨QF°ÕMH”⁄F£¨‘ÚÀƒ±þ–ŒHGQF «æÿ–Œ£¨
°ýFQ=HG£¨FH=QG£¨
Õ¨¿Ì£∫°˜BGQ°’°˜MFQ£¨
°ýQG=FQ=HG£¨BG=MF£¨
°þQH=1£¨
°ýGQ=GH=![]() £¨
£¨
°ýMH=BG+FH=![]() £¨
£¨
°ýMHµƒ»°÷µ∑∂Œß «![]() .
.


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏