ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΦΉΥυ ΨΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() Θ§
Θ§![]() ΝΫΒψΘ§”κ
ΝΫΒψΘ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() ΈΣΗΟ≈ΉΈοœΏΒΡΕΞΒψΘ°
ΈΣΗΟ≈ΉΈοœΏΒΡΕΞΒψΘ°
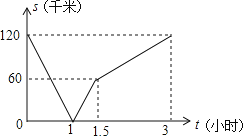
Θ®1Θ©»γΆΦΦΉΘ§Βψ![]() ΈΣ≈ΉΈοœΏ…œ
ΈΣ≈ΉΈοœΏ…œ![]() Θ§
Θ§![]() ΝΫΒψΦδΒΡ“ΜΕ·ΒψΘ§Ν§Ϋ”
ΝΫΒψΦδΒΡ“ΜΕ·ΒψΘ§Ν§Ϋ”![]() Θ§
Θ§![]() Θ§Β±
Θ§Β±![]() ΟφΜΐΉν¥σ ±Θ§‘ΎΕ‘≥Τ÷α…œ”–“ΜΕ·Βψ
ΟφΜΐΉν¥σ ±Θ§‘ΎΕ‘≥Τ÷α…œ”–“ΜΕ·Βψ![]() Θ§»γΆΦ““Υυ ΨΘ§ΙΐΒψ
Θ§»γΆΦ““Υυ ΨΘ§ΙΐΒψ![]() Ής
Ής![]() ÷αΫΜ
÷αΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§
Θ§![]() Θ§«σ
Θ§«σ![]() ΒΡΉν–Γ÷ΒΘ§≤Δ«σ≥ω¥Υ ±Βψ
ΒΡΉν–Γ÷ΒΘ§≤Δ«σ≥ω¥Υ ±Βψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
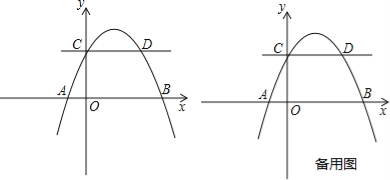
Θ®2Θ©»γΆΦ±ϊΥυ ΨΘ§ΫΪ![]() »ΤΉ≈Βψ
»ΤΉ≈Βψ![]() –ΐΉΣΘ§ΒΟΒΫ
–ΐΉΣΘ§ΒΟΒΫ![]() Θ§‘Ύ–ΐΉΣΙΐ≥Χ÷–Θ§ «Ζώ¥φ‘ΎΡ≥Ηω ±ΩΧ Ι“‘Βψ
Θ§‘Ύ–ΐΉΣΙΐ≥Χ÷–Θ§ «Ζώ¥φ‘ΎΡ≥Ηω ±ΩΧ Ι“‘Βψ![]() ΈΣΕΞΒψΒΡ»ΐΫ«–ΈΈΣ“‘
ΈΣΕΞΒψΒΡ»ΐΫ«–ΈΈΣ“‘![]() ΈΣ―ϋΒΡΒ»―ϋ»ΐΫ«–ΈΘ§»γΙϊ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ω¥Υ ±Βψ
ΈΣ―ϋΒΡΒ»―ϋ»ΐΫ«–ΈΘ§»γΙϊ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ω¥Υ ±Βψ![]() ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
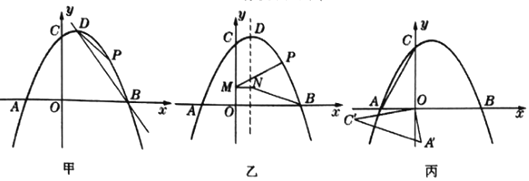
ΓΨ¥πΑΗΓΩΘ®1Θ©![]()
![]() ΘΜ
ΘΜ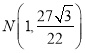 ΘΜΘ®2Θ©
ΘΜΘ®2Θ©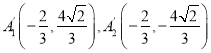 Θ§
Θ§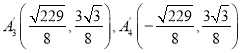 Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΙΐΒψ![]() Ής
Ής![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§”…
Θ§”…![]() ΟφΜΐΉν¥σΘ§ΒΟΒΫ
ΟφΜΐΉν¥σΘ§ΒΟΒΫ![]() Ήν¥σΘ§άϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ ΒΟΒΫΒψ
Ήν¥σΘ§άϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ ΒΟΒΫΒψ![]() ΒΡΉχ±ξΘ§ΫΪ
ΒΡΉχ±ξΘ§ΫΪ![]() œρΉσΤΫ“Τ“ΜΗωΒΞΈΜΘ§ ΙΒψ
œρΉσΤΫ“Τ“ΜΗωΒΞΈΜΘ§ ΙΒψ![]() ”ΎΒψ
”ΎΒψ![]() ÷ΊΚœΘ§Βψ
÷ΊΚœΘ§Βψ![]() ¬δ‘Ύ
¬δ‘Ύ![]() ÷α…œΒΡΒψ
÷α…œΒΡΒψ![]() ¥ΠΘ§Βψ
¥ΠΘ§Βψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ÷αΕ‘≥ΤΒΡΒψΈΣ
÷αΕ‘≥ΤΒΡΒψΈΣ![]() Θ§¥Υ ±
Θ§¥Υ ±![]() Ήν–ΓΘ§Ήν–Γ÷ΒΈΣ
Ήν–ΓΘ§Ήν–Γ÷ΒΈΣ![]() Θ§¥”ΕχΩ…ΒΟ¥πΑΗΘ§
Θ§¥”ΕχΩ…ΒΟ¥πΑΗΘ§
Θ®2Θ©–ΐΉΣΙΐ≥Χ÷–Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΘ§Β±![]() ±Θ§…η
±Θ§…η![]() Θ§Ιΐ
Θ§Ιΐ![]() Ής
Ής![]() ”Ύ
”Ύ![]() Θ§Ιΐ
Θ§Ιΐ![]() Ής
Ής![]() ”Ύ
”Ύ![]() άϊ”ΟœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ±μ Ψ
άϊ”ΟœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ±μ Ψ![]() ΒΡΉχ±ξΘ§άϊ”ΟΙ¥Ι…Ε®άμΫ®ΝΔΖΫ≥ΧΉι«σΫβΩ…ΒΟ¥πΑΗΘ§Β±
ΒΡΉχ±ξΘ§άϊ”ΟΙ¥Ι…Ε®άμΫ®ΝΔΖΫ≥ΧΉι«σΫβΩ…ΒΟ¥πΑΗΘ§Β±![]() Ά§άμΩ…ΒΟ¥πΑΗΘ°
Ά§άμΩ…ΒΟ¥πΑΗΘ°
ΫβΘΚΘ®1Θ©ΙΐΒψ![]() Ής
Ής![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]()
…η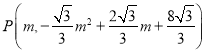 Θ§
Θ§
![]() Θ§
Θ§
![]() Β±
Β±![]()
![]()
Νν![]()
![]()
![]()
ΫβΒΟΘΚ![]()
![]()
…η![]() ΈΣ
ΈΣ![]()
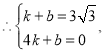
ΫβΒΟΘΚ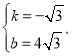
![]() ΈΣ
ΈΣ![]()
![]()
![]() Θ°
Θ°
![]()
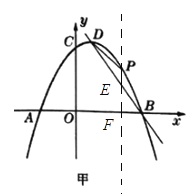
![]()
ΓύΒ±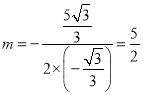 ±Θ§
±Θ§![]() Ήν¥σΘ§¥Υ ±
Ήν¥σΘ§¥Υ ±![]() ΒΡΟφΜΐ“≤Ήν¥σΘ°
ΒΡΟφΜΐ“≤Ήν¥σΘ°
¥Υ ±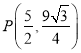
ΫΪ![]() œρΉσΤΫ“Τ“ΜΗωΒΞΈΜΘ§ ΙΒψ
œρΉσΤΫ“Τ“ΜΗωΒΞΈΜΘ§ ΙΒψ![]() ”ΎΒψ
”ΎΒψ![]() ÷ΊΚœΘ§Βψ
÷ΊΚœΘ§Βψ![]() ¬δ‘Ύ
¬δ‘Ύ![]() ÷α…œΒΡΒψ
÷α…œΒΡΒψ![]() ¥ΠΘ§
¥ΠΘ§
Βψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ÷αΕ‘≥ΤΒΡΒψΈΣ
÷αΕ‘≥ΤΒΡΒψΈΣ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΫΜ
ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() ΙΐΒψ
ΙΐΒψ![]() Ής
Ής![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§
Θ§
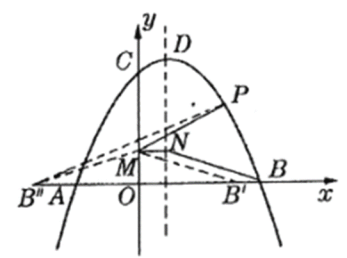
¥Υ ±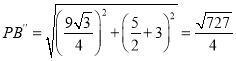
![]()
![]()
![]() Θ§
Θ§
![]()
![]() ΈΣ
ΈΣ![]() Θ§
Θ§
![]()
¥Υ ±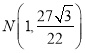
Θ®2Θ©”…Χβ“β÷ΣΘΚ![]()
![]()
Β±![]() ±Θ§
±Θ§
»γΆΦΘ§…η![]() Θ§Ιΐ
Θ§Ιΐ![]() Ής
Ής![]() ”Ύ
”Ύ![]() Θ§Ιΐ
Θ§Ιΐ![]() Ής
Ής![]() ”Ύ
”Ύ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
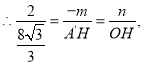
![]()
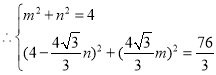
ΫβΒΟΘΚ
![]() Μρ
Μρ![]()
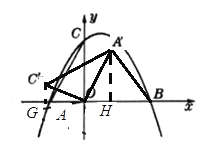
»γΆΦΘ§Β±![]()
Ά§άμΩ…ΒΟΘΚ
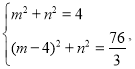
ΫβΒΟΘΚ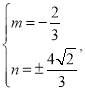
![]() Μρ
Μρ![]() Θ§
Θ§
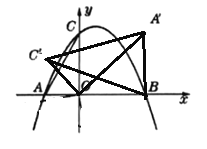
Ήέ…œΘΚ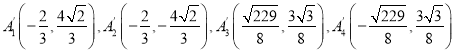

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ