题目内容
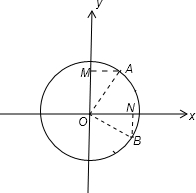
如图，钟表圆周上点A的横坐标是2，则圆周上点B的坐标为______．
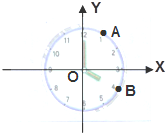
过点A作AM⊥y轴于点M，连接OA，
连接OB，过点B作BN⊥x轴，
由已知钟表得∠AOM=
=30°，
点A的横坐标是2，∴AM=2，
所以在直角三角形AOM中，
OA=2AM=4，
∴OB=OA=4，
同理∠BON=30°，
∴在直角三角形BNO中，
BN=
OB=2，
ON=OB•cos30°=4×
=2
，
∴点B的坐标为：（2
，-2），
故答案为：（2
，-2）．
连接OB，过点B作BN⊥x轴，
由已知钟表得∠AOM=
| 360° |
| 12 |
点A的横坐标是2，∴AM=2，
所以在直角三角形AOM中，
OA=2AM=4，
∴OB=OA=4，
同理∠BON=30°，
∴在直角三角形BNO中，
BN=
| 1 |
| 2 |
ON=OB•cos30°=4×
| ||
| 2 |
| 3 |
∴点B的坐标为：（2
| 3 |
故答案为：（2
| 3 |
练习册系列答案
考前必练系列答案
相关题目
