Question

【题目】在半圆O中，AB为直径，AC、AD为两条弦，且∠CAD+∠CAB＝90°．

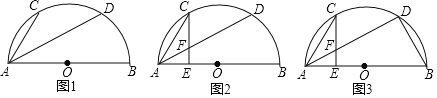
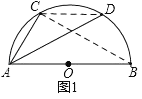
（1）如图1，求证：弧AC等于弧CD；

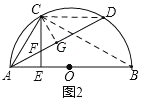
（2）如图2，点E在直径AB上，CE交AD于点F，若AF＝CF，求证：AD＝2CE；

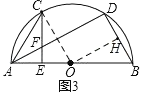
（3）如图3，在（2）的条件下，连接BD，若AE＝4，BD＝12，求弦AC的长．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）4．

【解析】

（1）如图1，连接BC、CD，先证∠CBA＝∠CAD，再证∠CDA＝∠CAD，可得出AC＝CD，即可推出结论；

（2）过点C作CG⊥AD于点G，则∠CGA＝90°，证CG垂直平分AD，得出AD＝2AG，再证△ACG≌△CAE，推出AG＝CE，即可得出AD＝2CE；

（3）取BD中点H，连接OH、OC，则BH＝DH＝BD＝6，OH⊥BD，证Rt△OEC≌Rt△BHO，推出OE＝BH＝6，OC＝OA＝10，则在Rt△OEC中，求出CE的长，在Rt△AEC中，可求出AC的长．

（1）证明：连接BC、CD，

∵AB是⊙O的直径，

∴∠ACB＝90°，

∴∠CAB+∠CBA＝90°，

∵∠CAB+∠CAD＝90°，

∴∠CBA＝∠CAD，

又∵∠CDA＝∠CBA，

∴∠CDA＝∠CAD，

∴AC＝CD，

∴ ；

（2）过点C作CG⊥AD于点G，则∠CGA＝90°，

由（1）知AC＝CD，

∴CG垂直平分AD，

∴AD＝2AG，

∵AF＝CF，

∴∠CAD＝∠ACE，

∵∠CAD+∠CAB＝90°，

∴∠ACE+∠CAB＝90°，

∴∠AEC＝90°＝∠CGA，

∵AC＝CA，

∴△ACG≌△CAE（AAS），

∴AG＝CE，

∴AD＝2CE；

（3）取BD中点H，连接OH、OC，则BH＝DH＝BD＝6，OH⊥BD，

∴∠OHB＝90°＝∠CEO，

∵OA＝OB，

∴OH是△ABD的中位线，

∴AD＝2OH，

由（2）知AD＝2CE，

∴OH＝CE，

∵OC＝OB，

∴Rt△OEC≌Rt△BHO（HL），

∴OE＝BH＝6，

∴OC＝OA＝AE+OE＝4+6＝10，

∴在Rt△OEC中，CE2＝OC2﹣OE2＝82，

∴在Rt△AEC中，AC＝ ＝4．