��Ŀ����
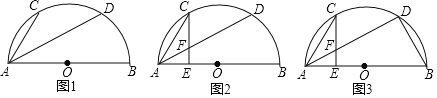
����Ŀ���ڡ�ABC�У�BC��6��S��ABC��18��������DEFG�ı�FG��BC�ϣ�����D��E�ֱ���AB��AC�ϣ�
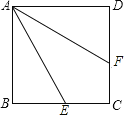
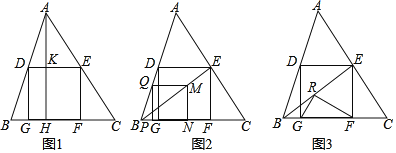
��1����ͼ1������A��AH��BC�ڵ�H����DE�ڵ�K����������DEFG�ı߳���
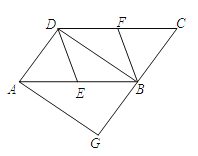
��2����ͼ2����BE��ȡ��M����MN��BC�ڵ�N��MQ��DE��AB�ڵ�Q��QP��BC�ڵ�P����֤���ı���MNPQ�������Σ�
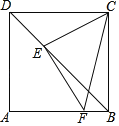
��3����ͼ3����BE��ȡ��R��ʹRE��FE������RG��RF����tan��EBF��![]() ����֤����GRF��90����
����֤����GRF��90����
���𰸡���1��3����2������������3��������
��������
��1����ͼ1�У���������DEFG�ı߳�Ϊx���������������εĶ�Ӧ�ߵıȵ������Ʊȹ������̼��ɽ�����⣮
��2������ƽ���߷��߶γɱ�������֤��MN��MQ����֤���ı���MNPQ��ƽ���ı��μ��ɽ�����⣮
��3����EF��GF��3k��BF��4k����BG��k��BE��5k���ɵ�BR2��BGBF��4k2���Ƴ�![]() ���Ƴ���RBG�ס�FBR���Ƴ���BRG����RFB����֤����ERF+��BRG��90���ɵý��ۣ�
���Ƴ���RBG�ס�FBR���Ƴ���BRG����RFB����֤����ERF+��BRG��90���ɵý��ۣ�
�⣺��1����ͼ1�У���������DEFG�ı߳�Ϊx��
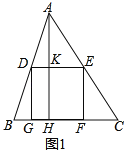
��AH��BC��
��S��ABC��![]() BCAH��18��
BCAH��18��
��![]() ��6��AH��18��
��6��AH��18��
��AH��6��
���ı���DEFG�������Σ�
��DE��BC��
���ADE�ס�ABC��
��![]() ��
��
��![]() ��
��
��x��3��
��������DEFG�ı߳�Ϊ3��
��2��֤������ͼ2�У�

��MN��BC���ı���DEFG�������Σ�
���MNB����EFB��90����DE��EF��
��MN��EF��
��![]() ��
��
��MQ��DE��
��![]() ��
��
��![]() ��
��
��MN��MQ��
��QP��BC��MN��BC��
��QP��MN��
��MQ��DE��DE��BC��
��QM��PN��
���ı���MNPQ��ƽ���ı��Σ�
�ߡ�MNP��90����
���ı���MNPQ�Ǿ��Σ�
��MN��MQ��
���ı���MNPQ�������Σ�
��3��֤������ͼ3�У�
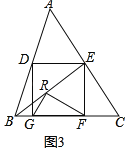
��Rt��EBF����tan��EBF��![]() ��
��
����Լ���EF��GF��3k��BF��4k����BG��k��BE��5k��
��ER��EF��3k��
��BR��BE��ER��2k��
��BR2��BGBF��4k2��
��![]() ��
��
�ߡ�RBG����RBF��
���RBG�ס�FBR��
���BRG����RFB��
��ER��EF��
���ERF����EFR��
�ߡ�EFR+��BFR��90����
���ERF+��BRG��90����
���FRG��90����

 ��У����ϵ�д�
��У����ϵ�д�