题目内容
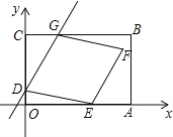
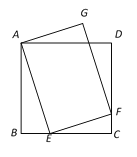
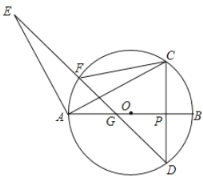
【题目】如图,点![]() 是
是![]() 直径
直径![]() 上的一点,过
上的一点,过![]() 作直线
作直线![]() ,分别交
,分别交![]() 于
于![]() ,
,![]() 两点,连接
两点,连接![]() ,并将线段
,并将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,分别交
,分别交![]() 和
和![]() 于
于![]() ,
,![]() ,连接
,连接![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)若点![]() 在直径
在直径![]() 上运动(不与点
上运动(不与点![]() ,
,![]() 重合),其它条件不变,请问
重合),其它条件不变,请问![]() 是否为定值?若是,请求出其值;若不是,请说明理由.
是否为定值?若是,请求出其值;若不是,请说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)是定值![]() ,理由见解析;
,理由见解析;
【解析】
(Ⅰ)连接AD,由同弧所对的圆周角相等可知∠ACF=∠ADF,由旋转的性质可知AC=AE,利用垂径定理证得AD=AC,推出AE=AD,∠AED=∠ADF,即可推出结论;
(Ⅱ)过点E作EN∥CD,过点D作DN⊥CD,且EN与直线AB交于点M,与直线DN交于点N,先证四边形MNDP是矩形,△EAM≌△ACP,推出MN=PD,MP=ND,EM=AP,AM=CP,再证明△END为等腰直角三角形,推出△EMG为等腰直角三角形,即可通过锐角三角函数推出结论.
解:(Ⅰ)连接![]() ,由同弧所对的圆周角相等可知∠ACF=∠ADF,
,由同弧所对的圆周角相等可知∠ACF=∠ADF,

∵AE是由线段AC绕点A逆时针旋转90°得到,
∴AC=AE,
∵CD⊥AB,
∴AB垂直平分CD,
∴AC=AD,
∴AE=AD,
∴∠AED=∠ADF,
∴∠ACF=∠AED;
(Ⅱ)是定值![]() ,
,
理由:过点E作EN∥CD,过点D作DN⊥CD,且EN与直线AB交于点M,与直线DN交于点N,
∵∠EAC=∠CPA=90°,
∴∠EAM+∠CAB=∠CAB+∠ACP=90°,
∴∠EAM=∠ACP,
∵DN⊥CD,CD⊥AB,
∴DN∥AB,
又∵EN∥CD,
∴四边形MNDP是矩形,
∴∠AME=∠APC=90°,
∵AC=AE,∠EAM=∠ACP,∠AME=∠APC,
∴△EAM≌△ACP,
∴EM=AP,AM=CP,
∵四边形MNDP是矩形,
∴MN=PD,MP=ND,
∵AB是直径,CD⊥AB,
∴MN=PD=CP=AM,
又∵EM=AP,
∴EM+MN=AP+AM,即EN=MP=ND,
∴△END是等腰直角三角形,
∴∠EDN=45°,
∵DN∥AB,
∴∠EGM=∠EDN=45°,
∴△EMG是等腰直角三角形,
∴![]() ,
,
∴![]() .
.