ЬтФПФкШн
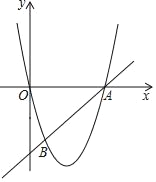
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпyЃНaЃЈx+2ЃЉЃЈxЉ6ЃЉЃЈaЃО0ЃЉгыxжсНЛгкCЃЌDСНЕуЃЈЕуCдкЕуDЕФзѓБпЃЉЃЌгыyжсИКАыжсНЛгкЕуAЃЎ
ШчЭМ1ЃЌХзЮяЯпyЃНaЃЈx+2ЃЉЃЈxЉ6ЃЉЃЈaЃО0ЃЉгыxжсНЛгкCЃЌDСНЕуЃЈЕуCдкЕуDЕФзѓБпЃЉЃЌгыyжсИКАыжсНЛгкЕуAЃЎ
ЃЈ1ЃЉШєЁїACDЕФУцЛ§ЮЊ16ЃЎ
ЂйЧѓХзЮяЯпНтЮіЪНЃЛ
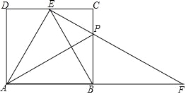
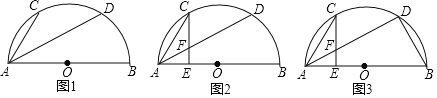
ЂкSЮЊЯпЖЮODЩЯвЛЕуЃЌЙ§SзїxжсЕФДЙЯпЃЌНЛХзЮяЯпгкЕуPЃЌНЋЯпЖЮSCЃЌSPШЦЕуSЫГЪБеыа§зЊШЮвтЯрЭЌЕФНЧЕНSC1ЃЌSP1ЕФЮЛжУЃЌЪЙЕуCЃЌPЕФЖдгІЕуC1ЃЌP1ЖМдкxжсЩЯЗНЃЌC1CгыP1SНЛгкЕуMЃЌP1PгыxжсНЛгкЕуNЃЎЧѓ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
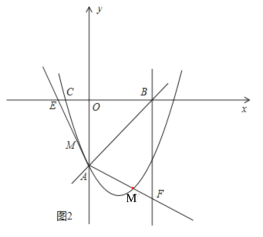
ЃЈ2ЃЉШчЭМ2ЃЌжБЯпyЃНxЉ12aгыxжсНЛгкЕуBЃЌЕуMдкХзЮяЯпЩЯЃЌЧвТњзуЁЯMABЃН75ЁуЕФЕуMгаЧвжЛгаСНИіЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉШєЁїACDЕФУцЛ§ЮЊ16ЃЎ
ЂйЧѓХзЮяЯпНтЮіЪНЃЛ
ЂкSЮЊЯпЖЮODЩЯвЛЕуЃЌЙ§SзїxжсЕФДЙЯпЃЌНЛХзЮяЯпгкЕуPЃЌНЋЯпЖЮSCЃЌSPШЦЕуSЫГЪБеыа§зЊШЮвтЯрЭЌЕФНЧЕНSC1ЃЌSP1ЕФЮЛжУЃЌЪЙЕуCЃЌPЕФЖдгІЕуC1ЃЌP1ЖМдкxжсЩЯЗНЃЌC1CгыP1SНЛгкЕуMЃЌP1PгыxжсНЛгкЕуNЃЎЧѓ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌжБЯпyЃНxЉ12aгыxжсНЛгкЕуBЃЌЕуMдкХзЮяЯпЩЯЃЌЧвТњзуЁЯMABЃН75ЁуЕФЕуMгаЧвжЛгаСНИіЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]() зюДѓжЕЮЊ2ЃЛЃЈ2ЃЉaЕФШЁжЕЗЖЮЇЮЊ
зюДѓжЕЮЊ2ЃЛЃЈ2ЃЉaЕФШЁжЕЗЖЮЇЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйЯШЧѓГіЕуAЃЌCЃЌDЕФзјБъЃЌДгЖјЕУCDЃН8ЃЌOAЃН12aЃЌНсКЯSЁїACDЃН16ЃЌМДПЩЧѓНтЃЛЂкИљОна§зЊЕФаджЪвдМАSASПЩжЄЃКP SP1C SC1ЃЌНјЖјжЄУїЁїMSCЁзЁїNSP1ЃЌЕУ![]() ЃЌЩшS(tЃЌ0)ЃЈ0ЁмtЁм6ЃЉЃЌПЩЕУ
ЃЌЩшS(tЃЌ0)ЃЈ0ЁмtЁм6ЃЉЃЌПЩЕУ![]() ЃЌНјЖјМДПЩЧѓНтЃЛ
ЃЌНјЖјМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЗжСНжжЧщПіЬжТлЃКЂйЕБЕуMдкyжсЕФзѓВрЪБЃЌДЫЪБЁЯMAOЃН30ЁуЃЌЧѓГіжБЯпAMЕФНтЮіЪНЃК![]() ЃЌНјЖјПЩЕУЕуMЕФКсзјБъЃЌСаГіЙигкaЕФВЛЕШЪНЃЌМДПЩЧѓНтЃЌЂкЕБЕуMдкyжсЕФгвВрЪБЃЌгУРрЫЦЕФЗНЗЈЃЌЧѓГіЕуMЕФКсзјБъЃЌСаГіЙигкaЕФВЛЕШЪНЃЌМДПЩЧѓНтЃЎ
ЃЌНјЖјПЩЕУЕуMЕФКсзјБъЃЌСаГіЙигкaЕФВЛЕШЪНЃЌМДПЩЧѓНтЃЌЂкЕБЕуMдкyжсЕФгвВрЪБЃЌгУРрЫЦЕФЗНЗЈЃЌЧѓГіЕуMЕФКсзјБъЃЌСаГіЙигкaЕФВЛЕШЪНЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉЂйгЩЬтвтЃЌСюyЃН0ЃЌНтЕУЃКx1ЃНЉ2ЃЌx2ЃН6ЃЌ
ЁрC(Љ2ЃЌ0)ЃЌD(6ЃЌ0)ЃЌ
ЁрCDЃН8ЃЎ
СюxЃН0ЃЌНтЕУЃКyЃНЉ12aЃЌЧвaЃО0ЃЌ
ЁрA(0ЃЌЉ12a)ЃЌМДOAЃН12aЃЌ
ЁрSЁїACDЃН![]() ЃН48aЃН16ЃЌ
ЃН48aЃН16ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃК![]() ЃЛ
ЃЛ
ЂкЁпЯпЖЮSCЃЌSPШЦЕуSЫГЪБеыа§зЊШЮвтЯрЭЌЕФНЧЕНSC1ЃЌSP1ЕФЮЛжУЃЌ
ЁрSC= SC1ЃЌSP= SP1ЃЌЁЯP SP1=ЁЯC SC1ЃЌ
ЁрP SP1C SC1ЃЈSASЃЉЃЌ
ЁрЁЯSP1P=ЁЯSC1CЃНЁЯSCC1ЃЌЧвЁЯMSCЃНЁЯNSP1ЃЌ
ЁрЁїMSCЁзЁїNSP1ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЩшS(tЃЌ0)ЃЈ0ЁмtЁм6ЃЉЃЌдђSP1=SPЃН![]() ЃЌSCЃНt+2ЃЌ
ЃЌSCЃНt+2ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп0ЁмtЁм6ЃЌ
ЁрЕБtЃН0ЪБЃЌ![]() зюДѓжЕЮЊ2ЃЛ
зюДѓжЕЮЊ2ЃЛ
ЃЈ2ЃЉЁпжБЯпyЃНxЉ12aгыxжсНЛгкЕуBЃЌ
ЁрB(12aЃЌ0)ЃЌOAЃНOBЃН12aЃЌЁЯOABЃНЁЯOBAЃН45Ёу,
ЂйЕБЕуMдкyжсЕФзѓВрЪБЃЌДЫЪБЁЯMAOЃН30ЁуЃЌ
ЩшжБЯпAMгыxжсНЛгкЕуEЃЌдђOEЃН![]() ЃЌ
ЃЌ
ЁрE(![]() ЃЌ0)ЃЌ
ЃЌ0)ЃЌ
гжЁпA(0ЃЌЉ12a)ЃЌ
ЁржБЯпAMЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
СЊСЂ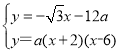 ЃЌ ЕУЃК
ЃЌ ЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрЕуMЕФКсзјБъЮЊЃК![]() ЃЌ
ЃЌ
Ёп![]() ЃМ0ЧвaЃО0ЃЌ
ЃМ0ЧвaЃО0ЃЌ
Ёр0ЃМaЃМ![]() ЃЛ
ЃЛ
ЂкЕБЕуMдкyжсЕФгвВрЪБЃЌзїЂйжажБЯпAEЙигкжБЯпABЕФЖдГЦжБЯпЃЌДЫЪБЃЌжБЯпAEЕФЖдГЦжБЯпгыХзЮяЯпЕФНЛЕуЃЌМДЮЊЕуMЃЌЙ§ЕуBзїxжсЕФДЙЯпгыжБЯпAEЙигкABЕФЖдГЦжБЯпНЛгкЕуFЃЌдђЁїEBAЁеЁїFBAЃЌ
ЁрЁЯBAFЃНЁЯBAE =75ЁуЃЌBFЃНBEЃН![]() ЃЌЁЯFBOЃН90ЁуЃЌ
ЃЌЁЯFBOЃН90ЁуЃЌ
ЁрF(12aЃЌ![]() )ЃЌ
)ЃЌ
ЁржБЯпAFЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
СЊСЂ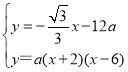 ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрЕуMЕФКсзјБъЮЊЃК![]() ЃЌ
ЃЌ
Ёп![]() ЧвaЃО0ЃЌ
ЧвaЃО0ЃЌ
ЁрaЃО![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃКЙЪвЊЪЙТњзуЁЯMABЃН75ЁуЕФЕуMгаЧвжЛгаСНИіЃЌдђaЕФШЁжЕЗЖЮЇЮЊЃК![]() ЃЎ
ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПФГаЃЦпФъМЖОйааЁАЪ§бЇМЦЫуФмСІЁББШШќЃЌБШШќНсЪјКѓЃЌЫцЛњГщВщВПЗжбЇЩњЕФГЩМЈЃЌИљОнГщВщНсЙћЛцжЦГЩШчЯТЕФЭГМЦЭМБэ
зщБ№ | ЗжЪ§x | ЦЕЪ§ |
A | 40ЁмxЃМ50 | 20 |
B | 50ЁмxЃМ60 | 30 |
C | 60ЁмxЃМ70 | 50 |
D | 70ЁмxЃМ80 | m |
E | 80ЁмxЃМ90 | 40 |
ИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЙВГщВщСЫЁЁЁЁУћбЇЩњЃЌЭГМЦЭМБэжаЃЌmЃНЁЁЁЁЃЌЧыВЙШЋжБЗНЭМЃЛ
ЃЈ2ЃЉЧѓЩШаЮЭГМЦЭМжаЁАBзщЁБЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШєЦпФъМЖЙВга800УћбЇЩњЃЌЗжЪ§ВЛЕЭгк60ЗжЮЊКЯИёЃЌЧыФуЙРЫуБОДЮБШШќШЋФъМЖКЯ
ИёбЇЩњЕФШЫЪ§