题目内容
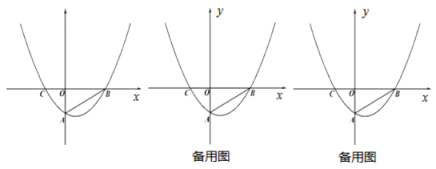
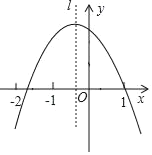
【题目】二次函数y＝ax2+bx+c（a≠0），经过点（1.0），对称轴l如图所示，若M＝a+b﹣c，N＝2a﹣b，P＝a+c，则M，N，P中，值小于0的数有（ ）个．
A.2B.1C.0D.3
【答案】A
【解析】
由二次函数y=ax2+bx+c（a≠0），经过点（1.0），和与y轴交点的位置，可以判断M的符号；由抛物线的开口方向和对称轴，可以判断N的符号；由抛物线的开口、对称轴的位置、和过（1，0）点可以判断P的符号，最后综合得出结论，做出选择．
解：（1）∵二次函数y＝ax2+bx+c（a≠0），经过点（1.0），
∴a+b+c＝0，
又∵抛物线与y轴交在y轴的正半轴，
∴c＞0
∴a+b﹣c＜0，故M＜0；
（2）抛物线开口向下，因此a＜0，对称轴在y轴左侧，﹣1的右侧，
∴﹣
＞﹣1，
∴2a﹣b＜0，故N＜0；
（3）抛物线开口向下，因此a＜0，对称轴在y轴左侧，因此a、b同号，∴b＜0
∵a+b+c＝0，
∴a+c=-b＞0，因此P＞0
综上所述：M＜0，N＜0，P＞0；
故选A．
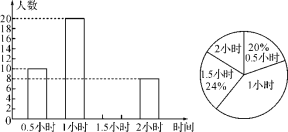
【题目】某校为调查“停课不停学”期间九年级学生平均每天上网课时长，随机抽取了
名九年级学生做网络问卷调查．共四个选项：
小时以下)、
小时)、
小时)， 
小时以上)，每人只能选一
项．并将调查结果绘制成如下不完整的统计表和统计图．
被调查学生平均每天上网课时间统计表
时长 | 所占百分比 |
|
|
|
|
|
|
|
|
合计 |
|
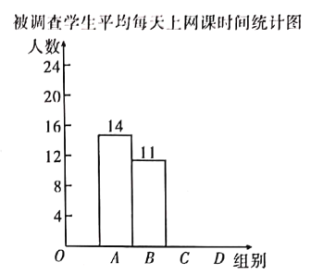
根据以上信息，解答下列问题：
，
，
补全条形统计图；
该校有九年级学生
名，请你估计仝校九年级学生平均每天上网课时长在
小时及以上的共多少名；
在被调查的对象中，平均每天观看时长超过
小时的，有
名来自九
班，
名来自九
班，其余都来自九
班，现教导处准备从
选项中任选两名学生进行电话访谈，请用列表法或画树状图的方法求所抽取的名学生恰好来自同一个班级的概率．
