题目内容
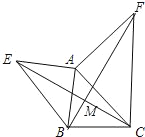
【题目】如图,已知∠ACB=90°,AC=BC,BD⊥DE,AE⊥DE,垂足分别为D、E.(这几何模型具备“一线三直角”)如下图:
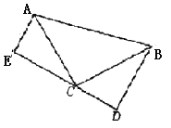
(1)①请你证明:△ACE≌△CBD;②若AE=3,BD=5,求DE的长;
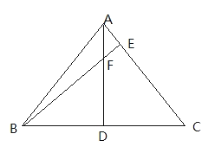
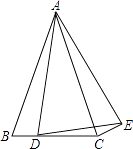
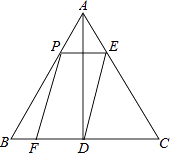
(2)迁移:如图:在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是边BC,AC上的点,将DE绕点D顺时针旋转90°,点E刚好落在边AB上的点F处,则CE=________。(不要求写过程)
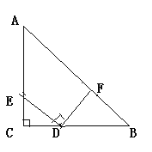
【答案】(1)①见解析;②DE=8;(2)CE=1.
【解析】
(1)如图1,根据垂直的定义和同角的余角相等得到∠E=∠D=90°,∠1=∠2,则结合已知条件AC=BC由AAS证得:△ACE≌△CBD;②如图2,同(1),证得△ACE≌△CBD,则根据全等三角形的对应边相等推知:CE=BD=4,AE=CD=2,故DE=CE﹣CD=4﹣2=2.(2) 过F作FM⊥BC于M,求出BM=MF,求出∠C=∠FMD,∠CED=∠MDF,证△CED≌△MDF,推出DM=CE,CD=FM=2即可.
(1)证明:如图1,∵BD⊥DE,AE⊥DE,
∴∠E=∠D=90°.
又∵∠ACB=90°,
∴∠1=∠2,
∴在△ACE与△CBD中,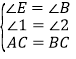 ,
,
∴△ACE≌△CBD(AAS);
②解:如图2,同(1),证得△ACE≌△CBD,
∴CE=BD=5,AE=CD=3,
∴DE=CE+CD=5+3=8.
(2)过F作FM⊥BC于M,
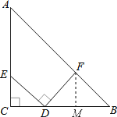
则∠FMB=∠FMD=90°,
∵∠C=90,AC=BC,
∴∠B=∠A=45°,
∴∠MFB=∠B=45°,
∴BM=MF,
∵DE⊥DF,
∴∠EDF=∠FMD=∠C=90°,
∴∠CED+∠CDE=90,∠CDE+∠FDM=90°,
∴∠CED=∠FDM,
在△CED和△MDF中,
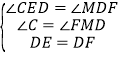 ,
,
∴△CED≌△MDF(AAS),
∵CD=2,BD=3,
∴DM=CE,CD=FM=2=BM,
∴CE=DM=32=1,
故答案为:1.