Question

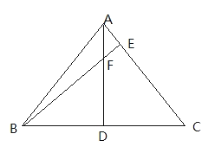
【题目】折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )

A. cm B. cm C. 12cm D. 13cm

Answer 1

【答案】A

【解析】

首先根据勾股定理求出BF的长度，进而求出CF的长度；再根据勾股定理求出EF的长度问题即可解决．

由题意得：AF=AD，EF=DE（设为x），∵四边形ABCD为矩形，

∴AF=AD=BC=10，DC=AB=8；∠ABF=90°；由勾股定理得：BF2=102－82=36，

∴BF=6，CF=10－6=4；在直角三角形EFC中，由勾股定理得：x2=42+（8－x）2，

解得：x=5， ∴AE2=102+52=125， ∴AE=5(cm)．故选A．