��Ŀ����
����Ŀ��ijͨѶ��˾�Ƴ�A��B�����ֻ������ײͣ��������ײ�ÿ�¶���һ���Ĺ̶����ú����ͨ��ʱ�䣬�������ͨ��ʱ��IJ����շѱ�Ϊ��A�ײ�aԪ/�֣�B�ײ�bԪ/�֣�ʹ��A��B�����ײ͵�ͨ������y��Ԫ����ͨ��ʱ��x���֣�֮��ĺ���ͼ����ͼ��ʾ��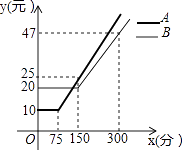
��1�����ֻ�ͨ��ʱ��Ϊ50����ʱ��д��A��B�����ײ͵�ͨ�����ã�
��2����a��b��ֵ��
��3����ѡ��B���ײͱ�A���ײ�����ʱ����ͨ��ʱ��x��ȡֵ��Χ��
���𰸡�
��1��
�⣺��ͼ���֪�����ֻ�ͨ��ʱ��Ϊ50����ʱ��A��B�����ײ͵�ͨ�����÷ֱ�Ϊ10Ԫ��20Ԫ��
��2��
�⣺a= ![]() =0.2��b=
=0.2��b= ![]() =0.18��
=0.18��
���ԣ�a��b��ֵ�ֱ���0.2��0.18��
��3��
�⣺A���ײͳ������ʱ��y��x�ĺ�����ϵʽΪy=0.2x��5��x��75����
��ͼ���֪����75��x��150ʱ����A��B�����ײ͵�ͨ������ͬ����0.2x��5=20��
���x=125��
�൱x��125ʱ��ѡ��B���ײ����㣮
����������1������ͼ����ã���2�����ݴ���ϵ����������ã���3�����������շ���ͬ�г����̣���⣬�����շ���ͬ��ʱ��ѡ��B�ײͣ�
�����㾫�������ڱ��⿼���ȷ��һ�κ����ı���ʽ����Ҫ�˽�ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ�������ܵó���ȷ�𰸣�