题目内容
【题目】某湖边健身步道全长1500米,甲、乙两人同时从同一起点匀速向终点步行.甲先到达终点后立刻返回,在整个步行过程中,甲、乙两人间的距离y(米)与出发的时间x(分)之间的关系如图中OA﹣AB折线所示.
(1)用文字语言描述点A的实际意义;
(2)求甲、乙两人的速度及两人相遇时x的值.
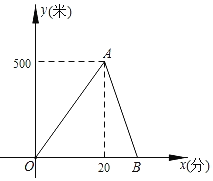
【答案】(1)20分钟时,甲乙两人相距500米;(2)甲的速度是每分钟75米,乙的速度是每分钟50米,两人相遇时x的值为24
【解析】
(1)根据题意结合图象解答即可;
(2)根据图象分别求出两人的速度,再根据题意列方程解答即可.
解:(1)点A的实际意义为:20分钟时,甲乙两人相距500米.
(2)根据题意得,![]() (米/分),
(米/分),![]() (米/分),
(米/分),
依题意,可列方程:75(x﹣20)+50(x﹣20)=500,
解这个方程,得 x=24,
答:甲的速度是每分钟75米,乙的速度是每分钟50米,两人相遇时x的值为24.

练习册系列答案
相关题目
【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.