题目内容
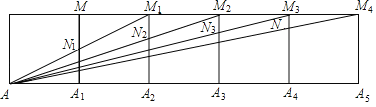
【题目】将2019个边长为1的正方形按如图所示的方式排列，点A，A1，A2，A3…A2019和点M，M1，M2…M2018是正方形的顶点，连接AM1，AM2，AM3…AM2018分别交正方形的边A1M，A2M1，A3M2…A2018M2017于点N1，N2，N3…N2018，四边形M1N1A1A2的面积是S1，四边形M2N2A2A3的面积是S2，…，则S2018为_____．
【答案】
【解析】
设左边第一个正方形左上角的顶点为O，先判定△M1MN1∽△M1OA，利用相似三角形的性质求出MN1的长，进而得出S1，同理得出S2，按照规律得出Sn，最后n取2018，计算即可得出答案．
解：如图所示，设左边第一个正方形左上角的顶点为O
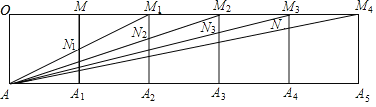
∵将2019个边长为1的正方形按如图所示的方式排列
∴OA∥MA1∥M1A2∥M2A3∥…∥M2018A2019
∴△M1MN1∽△M1OA
∴
，
∴
，
∴四边形M1N1A1A2的面积是
；
同理可得：
；
∴四边形M2N2A2A3的面积
；
…
∴四边形MnNnAnAn+1的面积
；
∴
；
故答案为：．
练习册系列答案
相关题目
【题目】某公司销售部有营业员
人，某一月的销售量统计如下表所示：
公司名营业员某一月的销售量统计表
月销售量/件数 | 1770 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 3 | 3 | 4 |
（1）求这名营业员该月销售量数据的平均数；
（2）这名营业员该月销售量数据的中位数是 件，众数是 件，为了提高大多数营业员的积极性，实行“每天定额售量，超出有奖”的措施．如果你是管理者，你选择．确定“定额”的统计量为 （填“中位数”或“众数”）
