题目内容
【题目】如图,这条花边中有4个圆和4个正三角形,且这条花边的总长度![]() 为4,则花边上正三角形的内切圆半径为()
为4,则花边上正三角形的内切圆半径为()

A.![]() B.
B.![]() C.1D.
C.1D.![]()
【答案】A
【解析】
画出图形,连接AD,OH,则AD过O,求出∠OHC=30°,求出DH,根据勾股定理即可求出内切圆半径OD.
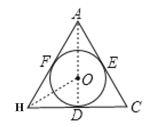
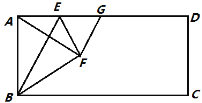
解:从中选择一个等边三角形和其内接圆如图,⊙O是△AHC的内切圆,⊙O切AH于F,切AC于E,切HC于D,
连接AD,OH,则AD过O(因为等边三角形的内切圆的圆心再角平分线上,也在底边的垂直平分线上),
∵△AHC是等边三角形,
∴∠AHC=60°,
∵⊙O是△AHC的内切圆,
∴∠OHC=![]() ∠AHC=30°,
∠AHC=30°,
∵HC=![]() AB=2,
AB=2,
∴HD=1,AH=2,
∴AD=![]() ,
,
在直角三角形OHD中,由勾股定理得:OD2+HD2=OH2 ,
得出:OD2+ 12 =(![]() -OD)2,
-OD)2,
∴OD=![]() (cm),
(cm),
故答案为:A

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
【题目】某公司销售部有营业员![]() 人,某一月的销售量统计如下表所示:
人,某一月的销售量统计如下表所示:
公司![]() 名营业员某一月的销售量统计表
名营业员某一月的销售量统计表
月销售量/件数 | 1770 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 3 | 3 | 4 |
(1)求这![]() 名营业员该月销售量数据的平均数;
名营业员该月销售量数据的平均数;
(2)这![]() 名营业员该月销售量数据的中位数是 件,众数是 件,为了提高大多数营业员的积极性,实行“每天定额售量,超出有奖”的措施.如果你是管理者,你选择.确定“定额”的统计量为 (填“中位数”或“众数”)
名营业员该月销售量数据的中位数是 件,众数是 件,为了提高大多数营业员的积极性,实行“每天定额售量,超出有奖”的措施.如果你是管理者,你选择.确定“定额”的统计量为 (填“中位数”或“众数”)