题目内容
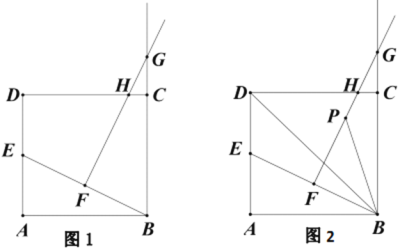
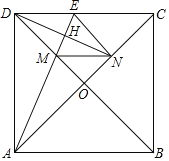
【题目】如图,已知在正方形ABCD中,对角线AC与BD交于点O,点M在线段OD上,联结AM并延长交边DC于点E,点N在线段OC上,且ON=OM,联结DN与线段AE交于点H,联结EN、MN.
(1)如果EN∥BD,求证:四边形DMNE是菱形;
(2)如果EN⊥DC,求证:AN2=NCAC.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据正方形性质及ON=OM,求出MN∥CD,进而得出四边形DMNE是平行四边形,在证明出△AOM≌△DON即可得到平行四边形DMNE是菱形;
(2)根据MN∥CD得到![]() ,再由EN⊥DC得到EN∥AD,
,再由EN⊥DC得到EN∥AD,![]() ,再由AB∥DC,得到
,再由AB∥DC,得到![]() ,即可得到
,即可得到![]() ,即为所求.
,即为所求.
证明:(1)如图1,
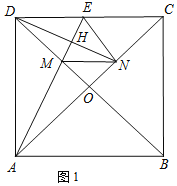
∵四边形ABCD是正方形,
∴OA=OB=OC=OD,AC⊥BD,
∵ON=OM,
∴![]() ,
,
∴MN∥CD,
又∵EN∥BD,
∴四边形DMNE是平行四边形,
在△AOM和△DON中,
∵∠AOM=∠DON=90°,OA=OD,OM=ON,
∴△AOM≌△DON(SAS),
∴∠OMA=∠OND,
∵∠OAM+∠OMA=90°,
∴∠OAM+∠OND=90°
∴∠AHN=90°.
∴DN⊥ME,
∴平行四边形DMNE是菱形;
(2)如图2,
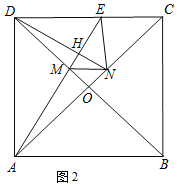
∵MN∥CD,
∴![]() ,
,
∵四边形ABCD是正方形,
∴AB∥DC,AB=DC,∠ADC=90°,
∴AD⊥DC,
又∵EN⊥DC,
∴EN∥AD,
∴![]() ,
,
∵AB∥DC,
∴![]() ,
,
∴![]() ,
,
∴AN2=NCAC.

练习册系列答案
相关题目