题目内容
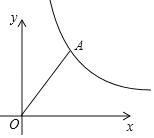
【题目】如图,已知反比例函数y=![]() (x>0)的图象经过点A(3,4),在该图象上找一点B,使tan∠BOA=
(x>0)的图象经过点A(3,4),在该图象上找一点B,使tan∠BOA=![]() ,则点B的坐标为_____.
,则点B的坐标为_____.
【答案】(2![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
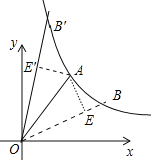
如图取点E(4,2),连接AE,OE.证明△ABE是直角三角形,tan∠BOA=![]() ,求出直线OE与反比例函数的图象的交点即可解决问题,再根据轴对称性可求出符合题意的另一点E’.
,求出直线OE与反比例函数的图象的交点即可解决问题,再根据轴对称性可求出符合题意的另一点E’.
如图取点E(4,2),连接AE,OE.
∵A(3,4),
∴OA=![]() =5,AE=
=5,AE=![]() =
=![]() ,OE=
,OE=![]() =2
=2![]() ,
,
∴OA2=AE2+OE2=25,
∴∠AEO=90°,
∴tan∠AOE=![]() =
=![]() ,
,
延长OE交反比例函数的图象于B,点B即为所求,
∵A(3,4)在y=![]() 上,
上,
∴k=12,
∵直线OE的解析式为y=![]() x,
x,
由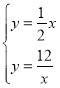 ,解得
,解得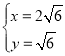 或
或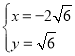 (舍弃),
(舍弃),
∴B(2![]() ,
,![]() ),
),
作点E关于直线OA的对称点E′,则E′(![]() ,
,![]() ),射线OE′交反比例函数的图象于B′,则点B′即为所求,
),射线OE′交反比例函数的图象于B′,则点B′即为所求,
∴直线OE′的解析式为y=![]() x,
x,
由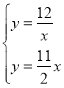 ,解得
,解得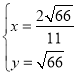 或
或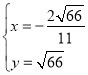 (舍弃),
(舍弃),
∴B′(![]() ,
,![]() ),
),
综上所述,满足条件的点B的坐标为(2![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
故答案为(2![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【点晴】
本题考查反比例函数图象上点的坐标特征,一次函数的应用等知识,解题的关键是学会寻找特殊点解决问题,学会构建一次函数,利用方程组确定交点坐标是解题的关键.

练习册系列答案
相关题目