Question

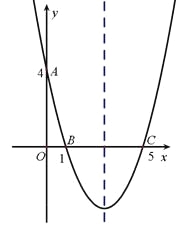
【题目】如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：

①4ac＜b2；

②3a+c＞0；

③方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3；

④当y＞3时，x的取值范围是0≤x＜2；

⑤当x＜0时，y随x增大而增大

其中结论正确的个数是（　　）

A.1个B.2个C.3个D.4个

Answer 1

【答案】C

【解析】

利用抛物线与x轴的交点个数可对①进行判断；由对称轴方程得到b＝﹣2a，然后根据x＝﹣1时函数值为0可得到3a+c＝0，则可对②进行判断；利用抛物线的对称性得到抛物线与x轴的一个交点坐标为（3，0），则可对③进行判断；根据抛物线在x轴上方所对应的自变量的范围可对④进行判断；根据二次函数的性质对⑤进行判断．

解：∵抛物线与x轴有2个交点，

∴b2﹣4ac＞0，所以①正确；

∵x＝＝1，即b＝﹣2a，

而x＝﹣1时，y＝0，即a﹣b+c＝0，

∴a+2a+c＝0，

所以②错误；

∵抛物线的对称轴为直线x＝1，

而点（﹣1，0）关于直线x＝1的对称点的坐标为（3，0），

∴方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3，

所以③正确；

根据对称性，由图象知，

当0＜x＜2时，y＞3，所以④错误；

∵抛物线的对称轴为直线x＝1，

∴当x＜1时，y随x增大而增大，所以⑤正确．

故选：C．