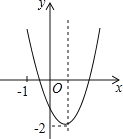题目内容
【题目】某宾馆有 50 个房间供游客居住，当每个房间的定价为每天 160 元时，房间会全部住满，当每个房间每天的定价每增加 10 元时，就会有一个房间空闲，如果游客居住房间， 宾馆需对每个房间每天支出 20 元的各种费用．设每个房间的定价为 x 元时，相应的住房数为 y 间．
（1）求 y 与 x 的函数关系式；
（2）定价为多少时宾馆当天利润 w 最大?并求出一天的最大利润；
（3）若老板决定每住进去一间房就捐出 a 元（a≤30）给当地福利院，同时要保证房间定价 x 在 160 元至 350 元之间波动时（包括两端点），利润 w 随 x 的增大而增大，求 a 的取值范围
【答案】（1）
；（2）定价为每间340元时，宾馆当天的利润最大为10240元；（3）
【解析】
（1）根据每天游客居住的房间数量=50-减少的房间数，即可解决问题；
（2）构造二次函数，利用二次函数的性质解决问题；
（3）构造二次函数，利用函数的增减性解决问题．
解：（1）
，
整理得：；
（2）
，
整理可得：
，
时w有最大值10240，
即定价为每间340元时，宾馆当天的利润最大为10240元；
（3）
，
整理得：
，
时w随x的增大而增大，
，
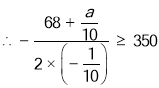解得：
，
，
．
通城学典默写能手系列答案【题目】在生活中，有很多函数并不一定存在解析式，对于这样的函数，我们可以通过列表和图象来对它可能存在的性质进行探索，例如下面这样一个问题：
已知y是x的函数，下表是y与x的几组对应值．
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孙同学根据学习函数的经验，利用上述表格反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．
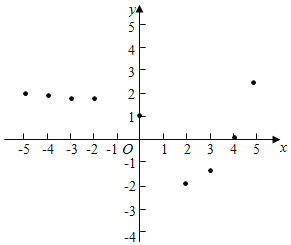
下面是小孙同学的探究过程，请补充完整；
（1）如图，在平面之间坐标系xOy中，描出了以上表中各对应值为坐标的点，根据描出的点，画出函数的图象：
（2）根据画出的函数图象回答：
①x＝﹣1时，对应的函数值y的为 ；
②若函数值y＞0，则x的取值范围是 ；
③写出该函数的一条性质（不能与前面已有的重复）： ．
