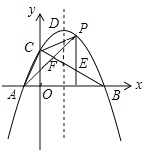ĖâÄŋÄÚČÝ
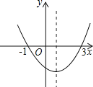
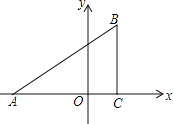
ĄūĖâÄŋĄŋŌŅÖŠĢšČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęÏĩÖÐĢŽĄũABCĘĮÖą―ĮČý―ĮÐÎĢŽĄÏACBĢ―90ĄãĢŽĩãAĢŽCĩÄŨøąę·ÖąðΊAĢĻĐ3ĢŽ0ĢĐĢŽCĢĻ1ĢŽ0ĢĐĢŽtanĄÏBACĢ―![]() ĢŪ
ĢŪ
ĢĻ1ĢĐÐīģöĩãBĩÄŨøąęĢŧ
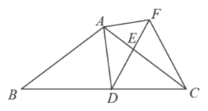
ĢĻ2ĢĐÔÚxÖáÉÏÕŌŌŧĩãDĢŽÁŽ―ÓBDĢŽĘđĩÃĄũADBÓëĄũABCÏāËÆĢĻēŧ°üĀĻČŦĩČĢĐĢŽēĒĮóĩãDĩÄŨøąęĢŧ
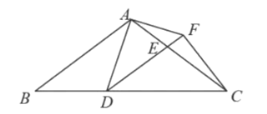
ĢĻ3ĢĐÔÚĢĻ2ĢĐĩÄĖõžþÏÂĢŽČįđûĩãPīÓĩãAģö·ĒĢŽŌÔ2cm/ÃëĩÄËŲķČŅØABÏōĩãBÔËķŊĢŽÍŽĘąĩãQīÓĩãDģö·ĒĢŽŌÔ1cm/ÃëĩÄËŲķČŅØDAÏōĩãAÔËķŊĢŪĩąŌŧļöĩãÍĢÖđÔËķŊĘąĢŽÁíŌŧļöĩãŌēËæÖŪÍĢÖđÔËķŊĢŪÉčÔËķŊĘąžäΊtĢŪÎĘĘĮ·ņīæÔÚÕâŅųĩÄtĘđĩÃĄũAPQÓëĄũADBÏāËÆĢŋČįīæÔÚĢŽĮëĮóģötĩÄÖĩĢŧČįēŧīæÔÚĢŽĮëËĩÃũĀíÓÉĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐĩãBĩÄŨøąęΊĢĻ1ĢŽ3ĢĐĢŧĢĻ2ĢĐĩãDĩÄŨøąęΊĢĻ![]() ĢŽ0ĢĐĢŧĢĻ3ĢĐīæÔÚĢŽĩątĢ―
ĢŽ0ĢĐĢŧĢĻ3ĢĐīæÔÚĢŽĩątĢ―![]() sŧō
sŧō![]() sĘąĢŽĄũAPQÓëĄũADBÏāËÆĢŪ
sĘąĢŽĄũAPQÓëĄũADBÏāËÆĢŪ
Ąū―âÎöĄŋ
ĢĻ1ĢĐļųūÝÕýĮÐĩÄķĻŌåĮóģöBCĢŽĩÃĩ―ĩãBĩÄŨøąęĢŧ
ĢĻ2ĢĐļųūÝĄũABCĄŨĄũADBĢŽĩÃĩ―![]() =
=![]() ĢŽīúČëžÆËãĮóģöADĢŽĩÃĩ―ĩãDĩÄŨøąęĢŧ
ĢŽīúČëžÆËãĮóģöADĢŽĩÃĩ―ĩãDĩÄŨøąęĢŧ
ĢĻ3ĢĐ·ÖĄũAPQĄŨĄũABDĄĒĄũAQPĄŨĄũABDÁ―ÖÖĮéŋöĢŽļųūÝÏāËÆČý―ĮÐÎĩÄÐÔÖĘÁÐĘ―žÆËãžīŋÉĢŪ
―âĢšĢĻ1ĢĐĄßAĢĻĐ3ĢŽ0ĢĐĢŽCĢĻ1ĢŽ0ĢĐĢŽ
ĄāACĢ―4ĢŽ
ĄßĄÏACBĢ―90ĄãĢŽtanĄÏBACĢ―![]() ĢŽ
ĢŽ
Ąā![]() Ģ―
Ģ―![]() ĢŽžī
ĢŽžī![]() Ģ―
Ģ―![]() ĢŽ
ĢŽ
―âĩÃĢŽBCĢ―3ĢŽ
ĄāĩãBĩÄŨøąęΊĢĻ1ĢŽ3ĢĐĢŧ
ĢĻ2ĢĐČįÍž1ĢŽŨũBDĄÍBA―ŧxÖáÓÚĩãDĢŽ
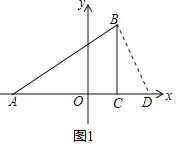
ÔōĄÏACBĢ―ĄÏABDĢ―90ĄãĢŽÓÖĄÏAĢ―ĄÏAĢŽ
ĄāĄũABCĄŨĄũADBĢŽ
Ąā![]() Ģ―
Ģ―![]() ĢŽ
ĢŽ
ÔÚRtĄũABCÖÐĢŽABĢ―![]() Ģ―
Ģ―![]() Ģ―5ĢŽ
Ģ―5ĢŽ
Ąā![]() Ģ―
Ģ―![]() ĢŽ
ĢŽ
―âĩÃĢŽADĢ―![]() ĢŽ
ĢŽ
ÔōODĢ―ADĐAOĢ―![]() ĢŽ
ĢŽ
ĄāĩãDĩÄŨøąęΊĢĻ![]() ĢŽ0ĢĐĢŧ
ĢŽ0ĢĐĢŧ
ĢĻ3ĢĐīæÔÚĢŽ
ÓÉĖâŌâĩÃĢŽAPĢ―2tĢŽAQĢ―![]() ĐtĢŽ
ĐtĢŽ
ĩąPQĄÍABĘąĢŽPQĄÎBDĢŽ
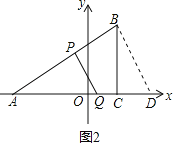
ĄāĄũAPQĄŨĄũABDĢŽ
Ąā![]() Ģ―
Ģ―![]() ĢŽžī
ĢŽžī![]() Ģ―
Ģ―![]() ĢŽ
ĢŽ
―âĩÃĢŽtĢ―![]() ĢŽ
ĢŽ
ĩąPQĄÍADĘąĢŽĄÏAQPĢ―ĄÏABDĢŽĄÏAĢ―ĄÏAĢŽ
ĄāĄũAQPĄŨĄũABDĢŽ
Ąā![]() Ģ―
Ģ―![]() ĢŽžī
ĢŽžī![]() Ģ―
Ģ―![]() ĢŽ
ĢŽ
―âĩÃĢŽtĢ―![]() ĢŽ
ĢŽ
ŨÛÉÏËųĘöĢŽĩątĢ―![]() sŧō
sŧō![]() sĘąĢŽĄũAPQÓëĄũADBÏāËÆĢŪ
sĘąĢŽĄũAPQÓëĄũADBÏāËÆĢŪ