题目内容
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是
上一点(不与C,D重合),∠CPD与∠COB有何大小关系?试说明理由;
(2)点P′在
上(不与C,D重合)时,∠CP′D与∠COB又有什么数量关系?为什么?

(1)P是
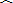 |
| CAD |
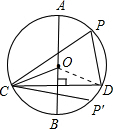
(2)点P′在
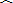 |
| CD |

(1)∠CPD=∠COB.…(1分)
理由:如图所示,连接OD.…(2分)
∵AB是直径,AB⊥CD,
∴
=
,…(3分)
∴∠COB=∠DOB=
∠COD.…(4分)
又∵∠CPD=
∠COD,
∴∠CPD=∠COB…(5分)
(2)∠CP'D与∠COB的数量关系是∠CP'D+∠COB=180°…(6分)
理由:∵∠CPD=
∠COD,∠CP'D=
(360°-∠COD)=180°-
∠COD,
∴∠CPD+∠CP'D=180°.…(8分)
由(1)知,∠CPD=∠COB,
∴∠CP'D+∠COB=180°.…(9分)
理由:如图所示,连接OD.…(2分)
∵AB是直径,AB⊥CD,
∴
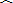 |
| BC |
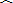 |
| BD |
∴∠COB=∠DOB=
| 1 |
| 2 |
又∵∠CPD=
| 1 |
| 2 |
∴∠CPD=∠COB…(5分)
(2)∠CP'D与∠COB的数量关系是∠CP'D+∠COB=180°…(6分)
理由:∵∠CPD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CPD+∠CP'D=180°.…(8分)
由(1)知,∠CPD=∠COB,
∴∠CP'D+∠COB=180°.…(9分)


练习册系列答案
相关题目







