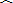题目内容
如图，在⊙O中弦AB⊥CD于点E，过E作AC的垂线交BD于点Q，P为垂足，求证Q为BD的中点．
证明：∵AB⊥CD于点E，过E作AC的垂线交BD于点Q，
∴三角形ACE、三角形PCE、三角形APE、三角形BED都是直角三角形．
∴∠DEQ=∠CEP（对顶角相等）．
∠CEP=∠A（同角的余角相等）．
又∵∠A=∠D（同弧所对的圆周角相等），
∴∠DEQ=∠D，∴EQ=QD（等角对等边）．
又∵∠QEB=∠B（等角的余角相等），
∴EQ=QB．
∴EQ=QD=QB，即Q为BD的中点．
∴三角形ACE、三角形PCE、三角形APE、三角形BED都是直角三角形．
∴∠DEQ=∠CEP（对顶角相等）．
∠CEP=∠A（同角的余角相等）．
又∵∠A=∠D（同弧所对的圆周角相等），
∴∠DEQ=∠D，∴EQ=QD（等角对等边）．
又∵∠QEB=∠B（等角的余角相等），
∴EQ=QB．
∴EQ=QD=QB，即Q为BD的中点．
练习册系列答案
提分百分百检测卷系列答案
相关题目
