题目内容
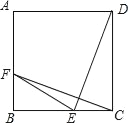
【题目】如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
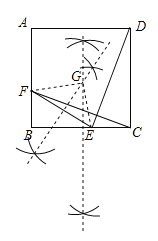
(1)请画出旋转中心G (保留画图痕迹),并连接GF,GE;
(2)若正方形的边长为2a,当CE= 时,S△FGE=S△FBE;当CE= 时,S△FGE=3S△FBE.
【答案】(1)见解析;(2)a ; ![]() 或
或![]()
【解析】
(1)根据旋转图形的性质,点C与点B是对应点,点E点F是对应点,分别作线段BC、EF的垂直平分线的交点就是旋转中心点G.
(2)由旋转的性质可以得出FG=EG,∠FGE=90°,设EC=x,利用勾股定理及三角形的面积公式建立等量关系,就可以求出结论.
(1)如图:分别作线段BC、EF的垂直平分线的交点就是旋转中心点G.
(2)∵G是旋转中心,且四边形ABCD是正方形,
∴FG=EG,∠FGE=90°
∵S△FGE=![]() ,且由勾股定理,得2FG2=EF2,
,且由勾股定理,得2FG2=EF2,
∴S△FGE=![]() ,
,
设EC=x,则BF=x,BE=2a-x,在Rt△BEF中,由勾股定理,得
EF2=x2+(2a-x)2,
∴S△FGE=![]() ,
,
∵S△FBE=![]() ,
,
①当S△FGE=S△FBE时,则
![]() ,
,
解得:x=a;
∴EC=a.
②当S△FGE=3S△FBE时,则![]() ,
,
∴2x2-4ax+a2=0,
解得:x=![]() 或x=
或x=![]() ,
,
∴EC=![]() 或EC=
或EC=![]() .
.
考查了旋转对称图形的性质,正方形的性质,三角形的面积及勾股定理的运用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目