题目内容
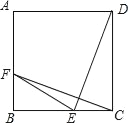
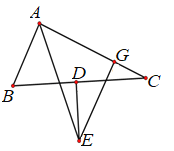
【题目】如图,在△ABC中,AE为∠BAC的角平分线,点D为BC的中点,DE⊥BC交AE于点E,EG⊥AC于点G.
(1)求证: AB+AC=2AG.
(2)若BC=8cm,AG=5cm,求△ABC的周长.
【答案】(1)见解析;(2)18cm
【解析】
(1)连接BE、EC,只要证明Rt△BFE≌Rt△CGE,得BF=CG,再证明Rt△AFE≌Rt△AGE得:AF=AG,根据线段和差定义即可解决.
(2由AG=5cm可得AB+AC=10cm即可得出△ABC的周长.
(1)延长AB至点M,过点E作EF⊥BM于点F

∵AE平分∠BAC
EG⊥AC于点G
∴EG=EF,∠EFB=∠EGC=90°
连接BE,EC
∵点D是BC的中点,DE⊥BC
∴BE=EC
在Rt△BFE与Rt△CGE中
![]()
∴Rt△BFE≌Rt△CGE(HL)
∴BF=GC
∵AB+AC=AB+AG+GC
∴AB+AC =AB+BF+AG
=AF+AG
在Rt△AFE与Rt△AGE中
![]()
∴Rt△AFE≌Rt△AGE(HL)
∴AF=AG
∴AB+AC=2AG
(2)∵AG=5cm, AB+AC=2AG
∴AB+AC=10cm
又∵BC=8cm
∴△ABC的周长为AB+AC+BC=8+10=18cm.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目