��Ŀ����
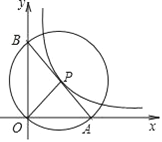
����Ŀ����ƽ��ֱ������ϵxOy�У�����Ϊ��C�����εĸ��߷ֱ�����������ƽ�У�����P����C���غϵĵ㣬��P���������εķ����Q�Ķ������£�������CP�������εı��ڵ�M��������CP�ϴ���һ��Q������CP+CQ��2CM�����QΪ��P���������εķ������ͼΪ��P���������εķ����Q��ʾ��ͼ��
�ر�أ�����P������C�غ�ʱ���涨CP��0��
��1���������ε�����Ϊԭ��O���߳�Ϊ2ʱ��
�ٷֱ��жϵ�F��2��0����G��![]() ��
��![]() ����H��3��3�����ڸ������εķ�����Ƿ���ڣ������ڣ�ֱ��д������������ꣻ
����H��3��3�����ڸ������εķ�����Ƿ���ڣ������ڣ�ֱ��д������������ꣻ
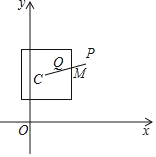
������P��ֱ��y����x+3�ϣ��ҵ�P���ڸ������εķ����Q���ڣ����P�ĺ������ȡֵ��Χ��
��2���������ε�����C��x���ϣ��߳�Ϊ2��ֱ��y��![]() ��x�ᡢy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ�õ�P���ڸ������εķ����Q�������ε��ڲ���ֱ��д�������ε�����C�ĺ������ȡֵ��Χ��
��x�ᡢy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ�õ�P���ڸ������εķ����Q�������ε��ڲ���ֱ��д�������ε�����C�ĺ������ȡֵ��Χ��
���𰸡���1���ٵ� F �ķ��������Ϊ��0��0������ G �ķ��������Ϊ����![]() ��
��![]() �����ڵ� P ��ֱ�� y=��x+3 �ϣ��ҵ� P ���ڸ������εķ���� Q ���ڣ��� P �ĺ������ȡֵ��Χ1��x��2����2�����������������ε����� C �ĺ������ȡֵ��ΧΪ 4��2
�����ڵ� P ��ֱ�� y=��x+3 �ϣ��ҵ� P ���ڸ������εķ���� Q ���ڣ��� P �ĺ������ȡֵ��Χ1��x��2����2�����������������ε����� C �ĺ������ȡֵ��ΧΪ 4��2![]() ��x��5��
��x��5��![]() �� 7��
�� 7��![]() ��x��8��
��x��8��
��������
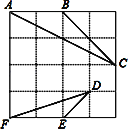
��1���ٸ��ݵ�P���������εķ����Ķ����֪��������������ABCD���߳�Ϊ4������Ϊԭ��O�����ڲ�ʱ�����������εı��ϣ��з���㣬�۲�ͼ���֪����F����G�з���㣬���ݶ��弴�ɽ�����⣻
����ͼ2�У�ֱ��y=-x+3��CD��K��1��2������BC��H��2��1�����۲�ͼ���жϣ�
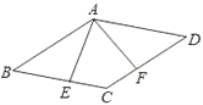
��2����ͼ3�У�������A��0��2![]() ����B��6��0��������ĸ�����λ�õĵ�C�����꼴���жϣ�
����B��6��0��������ĸ�����λ�õĵ�C�����꼴���жϣ�
��1������ͼ 1 �У�
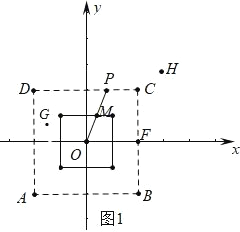
���ݵ�P ���������εķ����Ķ����֪�������������� ABCD���߳�Ϊ 4 ����Ϊԭ�� O�����ڲ�ʱ�����������εı��ϣ����з���㣬
�۲�ͼ���֪���� F���� G �з���㣬
�� F �ķ��������Ϊ��0��0������ G �ķ��������Ϊ����![]() ��
��![]() ����
����
����ͼ 2 �У�
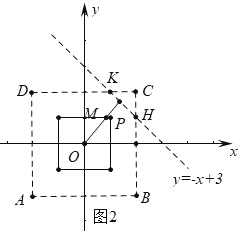
��ͼֱ�� y=��x+3 �� CD �� K��1��2������ BC �� H��2��1����
��� P ��ֱ�� y=��x+3 �ϣ��ҵ� P ���ڸ������εķ���� Q ���ڣ��� P �ĺ������ȡֵ��ΧΪ 1��x��2��
��2����ͼ 3 �У������� A��0��2![]() ����B��6��0����
����B��6��0����
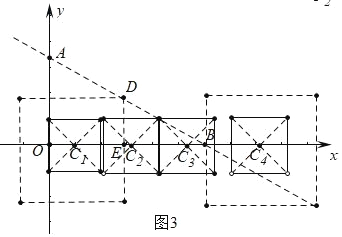
�ɣ�1����֪���߳�Ϊ 4 �������εĶ��� D ���߶� AB ��ʱ��DE=2��
��DE��OA��
��![]() ��
��
��![]() ��
��
��EB=2![]() ��OE=6��2
��OE=6��2![]() ��
��
��OC1=6��2![]() ��2=4��2
��2=4��2![]() ��
��
��C1��4��2![]() ��
��
���߳�Ϊ 2 �Ķ������߶� AB ��ʱ��C2��5��![]() ��0����C3��7��
��0����C3��7��![]() �������߳�Ϊ 4 �������εı߾����� B ʱ���ɵ� C4��8��0����
�������߳�Ϊ 4 �������εı߾����� B ʱ���ɵ� C4��8��0����
�۲�ͼ���֪�����������������ε����� C �ĺ������ȡֵ��ΧΪ 4��2![]() ��x��5��
��x��5�� ![]() �� 7��
�� 7��![]() ��x��8��
��x��8��

 53���ò�ϵ�д�
53���ò�ϵ�д�