题目内容
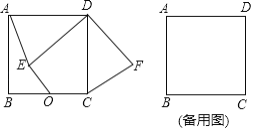
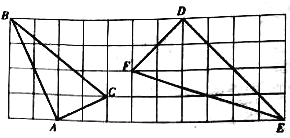
【题目】如图,在由边长均为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点(网格线的交点)上,请按要求完成下列各题.
(1)试证明△ABC是直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由.
【答案】(1)见解析;(2)相似.
【解析】
(1)由于小格都是正方形,可以利用勾股定理求得三角形各个边长,然后在利用勾股定理逆定理来证明是否为直角三角形;
(2)求出另一个三角形三条边的长,利用两个三角形对应边是否成比例可以验证两三角形是否是相似.
解:(1)根据图像,由勾股定理可分别求得:
AB=2![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,
(2)由勾股定理,可分别求得:
DE=4![]() ,FD=2
,FD=2![]() ,FE=
,FE=![]() ,
,
又由(1)可得:AB=2![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴![]() ,
,
∴△ABC和△DEF相似.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目