题目内容
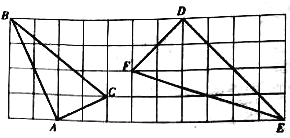
【题目】如图，将正方形网格放置在平面直角坐标系中，其中每个小正方形的边长均为1，△ABC经过平移后得到△A1B1C1，若AC上一点P（1.2，1.4）平移后对应点为P1，点P1绕原点顺时针旋转180°，对应点为P2，则点P2的坐标为（ ）
A. （2.8，3.6） B. （﹣2.8，﹣3.6）
C. （3.8，2.6） D. （﹣3.8，﹣2.6）
【答案】A
【解析】
根据平移的性质得出，△ABC的平移方向以及平移距离，即可得出P1坐标，进而利用中心对称图形的性质得出P2点的坐标．
∵A点坐标为：（1，1），A1（-3，-4），
∴△ABC向左平移了4个单位，向下平移了5个单位，
∴点P（1.2，1.4）平移后的对应点P1为：（-2.8，-3.6），
∵点P1绕点O逆时针旋转180°，得到对应点P2，
∴P2点的坐标为：（2.8，3.6）．
故选A．
练习册系列答案
相关题目
【题目】近视镜镜片的焦距
（单位：米）是镜片的度数
（单位：度）的函数，下表记录了一组数据：
| … | 100 | 250 | 400 | 500 | … |
| … | 1.00 | 0.40 | 0.25 | 0.20 | … |
（1）在下列函数中，符合上述表格中所给数据的是_________；
A．
B．
C．
D．
（2）利用（1）中的结论计算：当镜片的度数为200度时，镜片的焦距约为________米．