题目内容
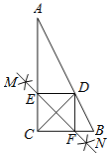
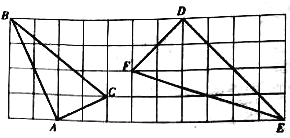
【题目】如图，正方形ABCD中，AB=
，O是BC边的中点，点E是正方形内一动点，OE=2，连接DE，将线段DE绕点D逆时针旋转90°得DF，连接AE，CF．
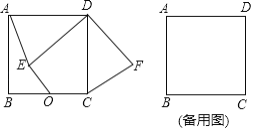
（1）求证：AE=CF；
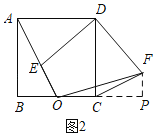
（2）若A，E，O三点共线，连接OF，求线段OF的长．
（3）求线段OF长的最小值．
【答案】（1）证明见解析；（2）
；（3）
【解析】
（1）根据旋转的性质，对应线段、对应角相等，可证明△ADE≌△CDF，即可得到AE＝CF；
（2）先利用
，求得
长，再利用
，求得
，然后设PF=x利用勾股定理求得x的值，即可求得OF的长；
（3）本题考査了利用三角形全等转化的思想解决问题．
（1）证明：如图1，由旋转得：
，
，
四边形
是正方形，
，
，
，
即
，
，
在
和
中，
，
，
；
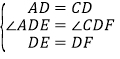（2）解：如图2，过
作
的垂线，交
的延长线于
，
的中点，且
，
，
，
三点共线，
，
由勾股定理得：
，
，
，
由（1）知：
，
，
，
，
，
，
，
，
，
设
，则
，
由勾股定理得：
，
或
（舍
，
，
，
由勾股定理得：
，
（3）解：如图3，由于
，所以点可以看作是以为圆心，2为半径的半圆上运动，
延长
到点，使得
，连接
，
，
，
，
，
当最小时，为、、三点共线，
，
，
的最小值是
．
练习册系列答案
阅读快车系列答案
相关题目
