题目内容
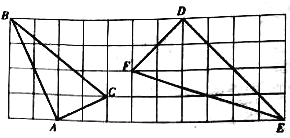
【题目】用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:
(1)求![]() 的值;
的值;
(2)这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;
(3)当![]() 时画出这个几何体的左视图.
时画出这个几何体的左视图.
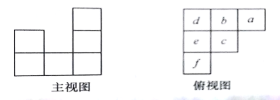
【答案】(1)a=3,b=1,c=1.(2)9个,11个.(3)详见解析
【解析】
(1)从此几何体的主视图中可以看出,最右边为三层,从俯视图中可以看出几何体的最右边只有一行,进而得出a的值,由主视图得中间只有一层,从俯视图看出几何体中间有两行,进而得出b、c的值;
(2)从(1)中得出几何体的中间和最右边的小正方体的个数是确定的,由俯视图得几何体的最底层有6个小正方体,从主视图中看出最左边有两层,所以最左边第二层最少1个,最多3个,进而解答即可;
(3)根据俯视图中小正方形上的数字,即可画出几何体的左视图.
根据题意作图:
(1)从此几何体的主视图中可以看出,几何体的最右边有三层,从俯视图中可以看出几何体的最右边只有一行,所以a=3,同理,从主视图可以看出几何体的中间只有一层,从俯视图看出几何体中间有两行,所以b=1,c=1.
(2)从俯视图可得出此几何体的最底层肯定需要6个小正方体,从主视图中看出此几何体最左边有两层,所以最左边最少需要再加1个,最多需要加3;
从(1)中得出几何体中中间和最右边的正方体数是确定的.所以要搭成此几何体至少需要6+1+0+2=9个正方体,最多需要6+1+1+1+0+2=11个正方体.
(3)根据题意画出几何体的左视图,如图所示.

 互动英语系列答案
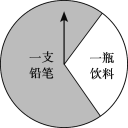
互动英语系列答案【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.
【题目】在二次函数y=-x2+bx+c中,函数y与自变量x的部分对应值如下表:
x | …… | -2 | 0 | 3 | 4 | …… |
y | …… | -7 | m | n | -7 | …… |
则m、n的大小关系为( )
A. m>n B. m<n C. m=n D. 无法确定