题目内容
【题目】类比、转化、从特殊到一般等思想方法在数学学习和研究中经常用到,如下是一个案例,请补充完整.
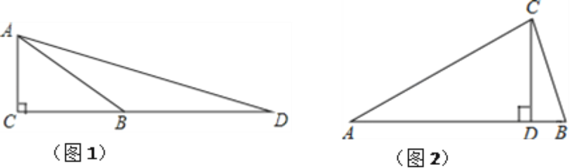
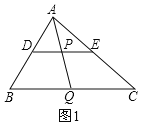
原题:如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P,求证:![]() =
=![]() .
.
(1)尝试探究:在图1中,由DP∥BQ,得△ADP___△ABQ(填“≌”或“∽”),则![]() =___,同理可得
=___,同理可得![]() =
=![]() ,从而
,从而![]() =
=![]() ;
;
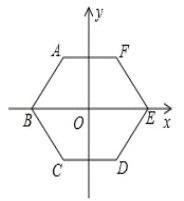
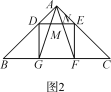
(2)类比延伸:如图2,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点,若AB=AC=1,则MN的长为_____;
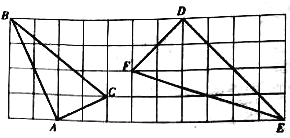
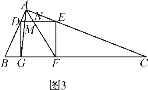
(3)拓展迁移:如图3,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点,AB<AC,求证:MN2=DM·EN.
【答案】(1)∽;![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)可证明△ADP∽△ABQ,△ACQ∽△ADP,从而根据等比代换,得出![]()
(2)根据三角形的面积公式求出BC边上的高![]() ,根据△ADE∽△ABC,求出正方形DEFG的边长
,根据△ADE∽△ABC,求出正方形DEFG的边长![]() ,根据
,根据![]() 等于高之比,即可求出MN;
等于高之比,即可求出MN;
(3)可得出△BGD∽△EFC,则DGEF=CFBG;又由DG=GF=EF,得![]() ,再根据(1)
,再根据(1)![]() ,从而得出答案.
,从而得出答案.
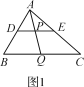
(1)如图1,
∵DP∥BQ,
∴△ADP∽△ABQ,
∴![]()
同理可得△ACQ∽△APE,
∴![]()
∴![]()
故答案为:∽;![]() ;
;
(2)如图2所示,
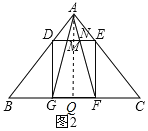
作AQ⊥BC于点Q.
∵BC边上的高![]()
且△ABC中,∠BAC=90°,正方形DEFG的四个顶点
∴DE=DG=GF=EF=BG=CF,
∴DE:BC=1:3,
又∵DE∥BC,
∴AD:AB=1:3,
∴![]()
∵DE边上的高为![]() ,
,![]()
∴![]()
∴MN=![]() .
.
(3)证明:
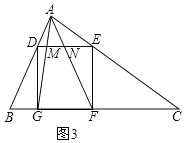
![]()
∵∠B+∠C=90°,∠CEF+∠C=90°,
∴∠B=∠CEF.
又∵∠BGD=∠EFC=90°,
∴△BGD∽△EFC.
∴![]() ,即DG·EF=CF·BG.
,即DG·EF=CF·BG.
又∵DG=GF=EF,∴GF2=CF·BG.
由(1)易得![]()
∴![]()
∴![]()
∵GF2=CF·BG,
∴MN2=DM·EN.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案