Question

【题目】我们知道，若线段上的个点把这条线段分制为两部分，其中较长的一部分与全长之比等于时，则这个点称为黄金分割点。类比三角形中线的定义，我们规定:连接三角形的一个顶点和它对边的黄金分割点的线段叫做该三角形的黄金分割线.

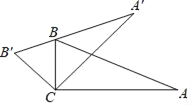
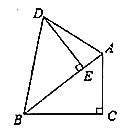
(1)如图1，CD是△ABC的黄金分割线(AD> BD)，△ABC的面积为4,求△ACD的面积 ；

(2)如图2,在△ABC中,∠A= 36°，AB=AC=1，过点B作BD平分∠ABC，与AC相交于点D，求证: BD是△ABC的黄金分割线.

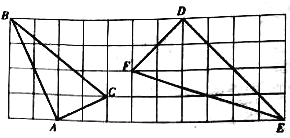
(3)如图3，BE、CD是△ABC的黄金分割线(AD> BD，AE> CE)，BE、CD相交于点O.

①设△BOD与△COE的面积分别为S1、S2 ,请猜想S1、S2之间的数量关系,并说明理由；

②求的值.

Answer 1

【答案】（1）2-2；（2）见解析；（3）①S1=S2；②.

【解析】

（1）设△ABC中AB边上的高为h，根据AD=AB，得出S△ACD=×ABh，从而可求出△ACD的面积；

（2）根据题意得出AD=BD=BC，求得△BCD∽△ABC，根据相似三角形的性质可得CD：BC=BC：AC，求得BC即可得解；

（3）①连接ED，根据题意得出S△ABE=S△ACD，即可得解；②求得△ADE∽△ABC，进一步求得△ODE∽△OCB，然后根据OD：OC=DE：BC=求解即可.

（1）根据题意可知：AD：AB=，设△ABC中AB边上的高为h，

则AD=AB，

∴S△ACD=ADh=×ABh=×4=2-2;

（2）∵∠A=36°，AB=AC，

∴∠ABC=∠C=72°，

∵过点B作BD平分∠ABC，与AC相交于点D，

∴∠CBD=∠A=36°，∠BDC=∠C=72°，

∴AD=BD=BC，

∴△BCD∽△ABC，

∴CD：BC=BC：AC，即，

解得BC=，

∴AD=，即D点是AC的黄金分割点，

∴BD是△ABC的黄金线；

（3）①S1=S2，理由如下：

如图，连接ED，

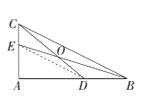
根据题意可得AD:AB=AE:AC=，

∴S△ABE:S△ABC=S△ACD:S△ABC=，

∴S△ABE=S△ACD，

∴S△COE=S△BOD，即S1=S2；

②由①得AD:AB=AE:AC，

又∵∠A是公共角，

∴△ADE∽△ABC，

∴∠DEA=∠BCA，DE:BC=AE:AC=，

∴DE∥BC，

∴△ODE∽△OCB，

∴OD:OC=DE:BC=，

∴OD:CD==.