题目内容
【题目】已知四边形ABCD为菱形,点E、F、G、H分别为各边中点,判断E、F、G、H四点是否在同一个圆上,如果在同一圆上,找到圆心,并证明四点共圆;如果不在,说明理由.
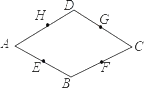
【答案】点E、F、G、H四点是以AC,BD的交点O为圆心的同一个圆上,证明见解析.
【解析】
根据菱形的对角线互相垂直,以及直角三角形斜边中线等于斜边的一半,得出E、F、G、H到O点距离都等于定长即可.
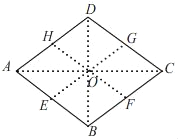
解:如图,
连接AC,BD相交于点O,连接OE,OF,OG,OH,
∵四边形ABCD是菱形,
∴AB=AD=CD=BC,AC⊥BD,
∵点E是AB的中点,
∴OE=![]() AB,
AB,
同理:OF=![]() BC,OG=
BC,OG=![]() CD,OH=
CD,OH=![]() AD,
AD,
∴OE=OF=OG=OH,
∴点E、F、G、H四点是以AC,BD的交点O为圆心的同一个圆上.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目