Question

【题目】作图题(不写作法，保留作图痕迹)

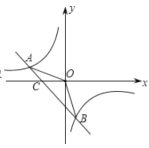
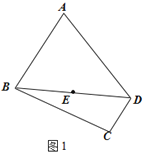
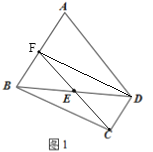
(一)如图1，在四边形ABCD中，CD∥AB，AB=2CD,BD=AD,E为BD中点,请仅用无刻度的直尺在图1中，画出△ABD的AB边上的高线DF．

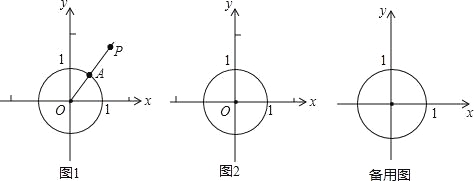
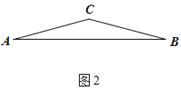
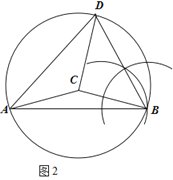
(二)如图2，已知等腰△ABC，∠ACB=150°．

(1)仅用没有无刻度的直尺和圆规作一个△ABD，使∠ADB=75°，∠ABD=60°.

(2)在⑴的前提下，连接CD，若AB=2+2．则CD的长为_______．

Answer 1

【答案】(一)见解析；(二)(1)见解析；(2).

【解析】

(一)连接CE交AB于F，连接DF；

(二) （1）以C为圆心，AC为半径画圆C，以B为圆心适当半径画弧，于AB要有交点，再以于AB的交点为圆心同样的半径画弧于刚才的弧交于一点，连接B与两个弧的交点即可得到∠ABD=60°，交圆C于D，连接AD即可得到∠ADB=75°；（2）设半径CD为先根据特殊角度算出AD、DB含的代数式，再根据余弦定理列出关于的方程，解得即可.

(一)连接CE交AB于F，连接DF.

(二)(1)以C为圆心，AC为半径画圆C尺规作∠ABD=60°

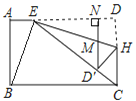
(2)过C点作CE⊥DA垂足为E，如图3所示：

设半径CD为

∵∠ABD=60°

∴∠ACD=120°

∴∠EDC=30°

∴

∵∠ADB=75°，∠ABD=60°

∴∠DAB=45°

∴∠DCB=90°

∴

根据余弦定理得：

代入各值解得：

解得：

即