题目内容
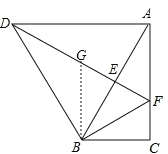
【题目】如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.

(1)求证:DA∥BC;
(2)猜想线段DF、AF的数量关系,并证明你的猜想.
【答案】(1)证明见解析;(2)猜想:DF=2AF,证明见解析.
【解析】
试题(1)利用等边三角形的判定与性质得出∠DAB=∠ABC,进而得出答案;
(2)首先利用旋转的性质以及全等三角形的判定方法得出△DBG≌△ABF(SAS),进而得出△BGF为等边三角形,求出DF=DG+FG=AF+AF=2AF.
试题解析:(1)由旋转的性质可知:∠DBE=∠ABC=60°,BD=AB,
∴△ABD为等边三角形,
∴∠DAB=60°,
∴∠DAB=∠ABC,
∴DA∥BC;
(2)猜想:DF=2AF,
证明如下:如图,在DF上截取DG=AF,连接BG,
由旋转的性质可知,DB=AB,∠BDG=∠BAF,
在△DBG和△ABF中,
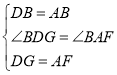 ,
,
∴△DBG≌△ABF(SAS),
∴BG=BF,∠DBG=∠ABF,
∵∠DBG+∠GBE=α=60°,
∴∠GBE+∠ABF=60°,即∠GBF=α=60°,
又∵BG=BF,
∴△BGF为等边三角形,
∴GF=BF,
又∵BF=AF,
∴FG=AF,
∴DF=DG+FG=AF+AF=2AF.

练习册系列答案
相关题目



