题目内容
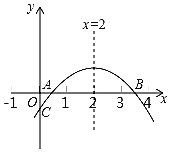
【题目】抛物线y=ax2+bx+c的顶点D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c>0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论是( )
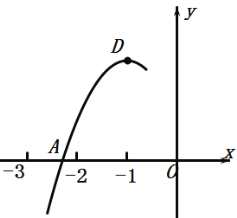
A.③④B.②④C.②③D.①④
【答案】A
【解析】
利用抛物线与x轴有2个交点和判别式的意义可对①进行判断;利用抛物线的对称性得到抛物线与x轴的另一个交点A在点(0,0)和(1,0)之间,则x=1时,a﹣b+c<0,则可对②进行判断;由抛物线的对称轴方程得到b=2a,而x=﹣1时,a﹣b+c=2,则a﹣2a+c=2,、于是可对③进行判断;利用抛物线y=ax2+bx+c的顶点D(﹣1,2),可得到抛物线与直线y=2只有一个公共点,于是可对④进行判断.
解:∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,所以①错误;
∵抛物线y=ax2+bx+c的顶点D(﹣1,2),
∴抛物线的对称轴为直线x=﹣1,
而抛物线与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,
∴抛物线与x轴的另一个交点A在点(0,0)和(1,0)之间,
∴x=1时,y<0,
∴a﹣b+c<0,所以②错误;
∵抛物线的对称轴为直线x=﹣![]() =﹣1,
=﹣1,
∴b=2a,
∵x=﹣1时,y=2,
即a﹣b+c=2,
∴a﹣2a+c=2,即c﹣a=2,所以③正确;
∵抛物线y=ax2+bx+c的顶点D(﹣1,2),
即x=﹣1时,y有最大值2,
∴抛物线与直线y=2只有一个公共点,
∴方程ax2+bx+c﹣2=0有两个相等的实数根,所以④正确.
故选:A.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 21 | 42% |
良好 | m | 40% |
合格 | 6 | n% |
待合格 | 3 | 6% |
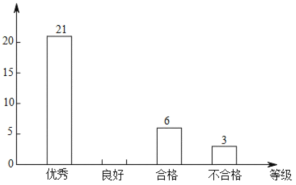
请根据以上信息,解答下列问题:
(1)本次调查随机抽取了 名学生;表中m= ,n= ;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.