Question

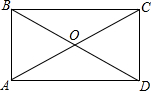
如图，P是矩形ABCD内一点，若PA=3，PB=4，PC=5，则PD=______．

Answer 1

过P作AB的平行线分别交DA、BC于E、F，过P作BC的平行线分别交AB、CD于G、H．
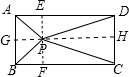设AG=DH=a，BG=CH=b，AE=BF=c，DE=CF=d，
则

AP2=a2+c2，CP2=b2+d2， BP2=b2+c2，DP2=d2+a2

于是AP²+CP²=BP²+DP²，又PA=3，PB=4，PC=5，
故DP²=AP²+CP²-BP²=3²+5²-4²=18，
则DP=3

2

．
故本题答案为3

2

．