题目内容
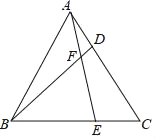
【题目】如图,△ABC是等边三角形,D,E分别是AC,BC边上的点,且AD=CE,连接BD,AE相交于点F.
(1)∠BFE的度数是多少;
(2)如果![]() ,那么
,那么![]() 等于多少;
等于多少;
(3)如果![]() 时,请用含n的式子表示AF,BF的数量关系,并证明.
时,请用含n的式子表示AF,BF的数量关系,并证明.
【答案】(1)∠BFE=60°;(2)![]() =1;(3)
=1;(3)![]() .证明见解析.
.证明见解析.
【解析】
(1)易证△ABD≌△ACE,可得∠DAF=∠ABF,根据外角等于不相邻两个内角的和即可解题.
(2)如图1中,当![]() =
=![]() 时,由题意可知:AD=CD,BE=CE.利用等腰三角形的性质即可解决问题;
时,由题意可知:AD=CD,BE=CE.利用等腰三角形的性质即可解决问题;
(3)设AF=x,BF=y,AB=BC=AC=n.AD=CE=1,由△ABD≌△CAE,推出BD=AE,设BD=AE=m,利用相似三角形的性质,列出关系式即可解决问题;
(1)∵△ABC是等边三角形,
∴AB=AC,∠BAD=∠C=60°,
在△ABD和△ACE中,
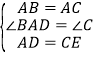 ,
,
∴△ABD≌△ACE(SAS)
∴∠DAF=∠ABD,
∴∠BFE=∠ABD+∠BAF=∠DAF+∠BAF=∠BAD=60°,
(2)如图1中,当![]() =
=![]() 时,由题意可知:AD=CD,BE=CE.
时,由题意可知:AD=CD,BE=CE.
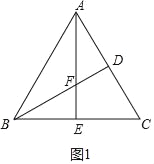
∵△ABC是等边三角形,BE=EC,AD=CD,
∴∠BAE=![]() ∠BAC=
∠BAC=![]() ×60°=30°,∠ABD=
×60°=30°,∠ABD=![]() ∠ABC=30°,
∠ABC=30°,
∴∠FAB=∠FBA,
∴FA=FB,
∴![]() =1.
=1.
(3)设AF=x,BF=y,AB=BC=AC=n.AD=CE=1,
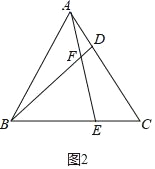
∵△ABD≌△CAE,
∴BD=AE,∠DAF=∠ABD,设BD=AE=m,
∵∠ADF=∠BDA,
∴△ADF∽△BDA,
∴![]() ,
,
∴![]() ①,
①,
∵∠FBE=∠CBD,∠BFE=∠C=60°,
∴△BFE∽△BCD,
∴![]() ,
,
∴![]() ②,
②,
①÷②得到:![]() ,
,
∴![]() .
.

练习册系列答案
相关题目