题目内容
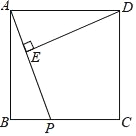
【题目】如图,在正方形ABCD中,AB=4,P是BC边上一动点(不与B,C重合),DE⊥AP于E.
(1)试说明△ADE∽△PAB;
(2)若PA=x,DE=y,请写出y与x之间的函数关系式.
【答案】(1)说明见解析;(2)y=![]() x(4<x<4
x(4<x<4![]() ).
).
【解析】
(1)根据正方形的性质以及DE⊥AP即可判定△ADE∽△PAB.
(2)根据相似三角形的性质即可列出y与x之间的关系式,需要注意的是x的范围.
解:(1)∵四边形ABCD为正方形,
∴∠BAD=∠ABC=90°,
∴∠EAD+∠BAP=90°,
∠BAP+∠APB=90°,
∴∠EAD=∠APB,
又∵DE⊥AP,∠AED=∠B=90°,
∴△ADE∽△PAB.
(2)由(1)知△PAB∽△ADE,
∴![]() ,
,
∴![]()
∴y=![]() x(4<x<4
x(4<x<4![]() ).
).

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目