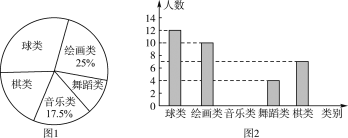
题目内容
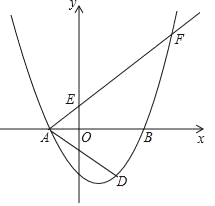
【题目】如图,在平面直角坐标系xOy中,已知抛物线y= ![]() 与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且
与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且![]() .
.
(1)求这条抛物线的表达式,并写出它的对称轴;
(2)求∠FAB的余切值;
(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.
【答案】抛物线的解析式为y=![]() .抛物线的对称轴为x=1;(2)
.抛物线的对称轴为x=1;(2)![]() ;(3)(0,6)或P(0,﹣
;(3)(0,6)或P(0,﹣![]() ).
).
【解析】试题分析:(1)根据代入法求出函数的解析式,然后根据对称轴的关系式求出对称轴;
(2)过点F作FM⊥x轴,垂足为M,设E(0,t),则OE=t,然后根据题意得到用t表示的F点的坐标,代入解析式可求得t的值,然后根据∠FAB的余切值;
(3)由C点的坐标求出D点的坐标,然后根据∠DAB的余切值求出∠DAB=∠BAF,然后分情况讨论:①当点P在AF的上方和②当点P在AF的下方,求出P点的坐标.
试题解析:(1)把C(0,﹣3)代入得:c=﹣3,
∴抛物线的解析式为y=![]() +bx﹣3.
+bx﹣3.
将A(﹣2,0)代入得:![]() ×(﹣2)2﹣2b﹣3=0,解得b=﹣
×(﹣2)2﹣2b﹣3=0,解得b=﹣![]() ,
,
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣3.
x﹣3.
∴抛物线的对称轴为x=﹣![]() =1.
=1.
(2)过点F作FM⊥x轴,垂足为M.
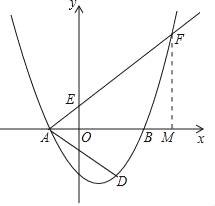
设E(0,t),则OE=t.
∵![]() ,
,
∴![]() =
=![]() =
=![]() .
.
∴F(6,4t).
将点F(6,4t)代入y=![]() x2﹣
x2﹣![]() x﹣3得:
x﹣3得:![]() ×62﹣
×62﹣![]() ×6﹣3=0,解得t=
×6﹣3=0,解得t=![]() .
.
∴cot∠FAB=![]() =
=![]() .
.
(3)∵抛物线的对称轴为x=1,C(0,﹣3),点D是点C关于抛物线对称轴的对称点,
∴D(2,﹣3).
∴cot∠DAB=![]() ,
,
∴∠FAB=∠DAB.
如下图所示:
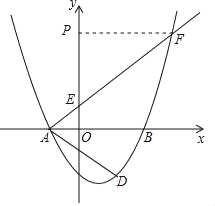
当点P在AF的上方时,∠PFA=∠DAB=∠FAB,
∴PF∥AB,
∴yp=yF=6.
由(1)可知:F(6,4t),t=![]() .
.
∴F(6,6).
∴点P的坐标为(0,6).
当点P在AF的下方时,如下图所示:
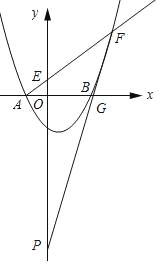
设FP与x轴交点为G(m,0),则∠PFA=∠FAB,可得到FG=AG,
∴(6﹣m)2+62=(m+2)2,解得:m=![]() ,
,
∴G(![]() ,0).
,0).
设PF的解析式为y=kx+b,将点F和点G的坐标代入得: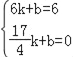 ,
,
解得:k=![]() ,b=﹣
,b=﹣![]() .
.
∴P(0,﹣![]() ).
).
综上所述,点P的坐标为(0,6)或P(0,﹣![]() ).
).