题目内容
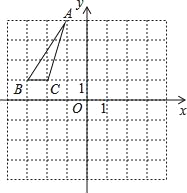
【题目】如图,一次函数y1=k1x+b的图象与反比例函数y2=![]() 的图象相交于A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=
的图象相交于A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=![]() .
.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积;
(3)请直接写出当x<m时,y2的取值范围.
【答案】(1)y2=-![]() ;(2)S△AOB=
;(2)S△AOB=![]() ;(3)当x<3时,y2>0或y2<-4.
;(3)当x<3时,y2>0或y2<-4.
【解析】
(1)过点A作AE⊥![]() 轴于点E,在Rt△AEO中,通过解直角三角形可求出点A的坐标,由反比例函数图象上点的坐标特征即可求出反比例函数的解析式;
轴于点E,在Rt△AEO中,通过解直角三角形可求出点A的坐标,由反比例函数图象上点的坐标特征即可求出反比例函数的解析式;
(2)由反比例函数图象上点的坐标特征可求出点B的坐标,根据点A、B的坐标,利用待定系数法可求出直线AB的解析式,再根据一次函数图象上点的坐标特征可求出点C的坐标,利用三角形的面积公式即可求出△AOB的面积;
(3)观察函数图象可得出:![]() <0以及0<
<0以及0<![]() <3时,
<3时,![]() 的取值范围,合在一起即可得出结论.
的取值范围,合在一起即可得出结论.
解:(1)过点A作AE⊥x轴于点E,如图所示.

在Rt△AEO中,AO=5,sin∠AOC=![]() ,
,
∴AE=AOsin∠AOC=5×![]() =3,
=3,
∴OE=![]() =4,
=4,
∴点A的坐标为(-4,3).
∵点A在反比例函数y2=![]() 的图象上,
的图象上,
∴k2=-4×3=-12,
∴反比例函数的解析式为y2=-![]() .
.
(2)∵点B(m,-4)反比例函数y2=-![]() 的图象上,
的图象上,
∴-4=-![]() ,解得:m=3,
,解得:m=3,
∴点B的坐标为(3,-4).
将A(-4,3)、B(3,-4)代入y1=k1x+b中,
![]() ,解得:
,解得:![]() ,
,
∴直线AB的解析式为y=-x-1.
当y=-x-1=0时,x=-1,
∴点C的坐标为(-1,0),
∴S△AOB=![]() OC(yA-yB)=
OC(yA-yB)=![]() ×1×[3-(-4)]=
×1×[3-(-4)]=![]() .
.
(3)观察函数图象可知:当x<0时,y2>0;当0<x<3时,y2<-4.
∴当x<3时,y2>0或y2<-4.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案